题目内容
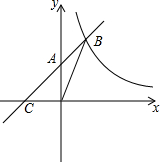 如图,一次函数y=ax+b(a≠0)图象交y轴于点A(0,2),且与反比例函数y=
如图,一次函数y=ax+b(a≠0)图象交y轴于点A(0,2),且与反比例函数y=| k |
| x |
(1)求反比例函数与一次函数的解析式;
(2)若一次函数与x轴交于C点,求△OBC的面积.
考点:反比例函数与一次函数的交点问题
专题:
分析:(1)把B的坐标代入反比例函数的解析式,然后根据三角形的面积公式求得m、k的值,然后利用待定系数法求得一次函数解析式.
(2)根据一次函数的解析式求得C的坐标,即可求得OC=2,然后根据三角形的面积公式即可求得.
(2)根据一次函数的解析式求得C的坐标,即可求得OC=2,然后根据三角形的面积公式即可求得.
解答:解:(1)由反比例函数过点B(m.4),得:4m=k,
由S△AOB=2得:
×2×m=2,即m=2,
则k=8,
则反比例函数的关系式为:y=
.
一次函数过点A(0,2),B(2,4),
得:
,解得
则一次函数的解析式为y=x+2.
(2)由直线y=x+2可知C(-2,0),
∴OC=2,
∴S△OBC=
OC•|yB|=
×2×4=4.
由S△AOB=2得:
| 1 |
| 2 |
则k=8,
则反比例函数的关系式为:y=
| 8 |
| x |
一次函数过点A(0,2),B(2,4),
得:
|
|
则一次函数的解析式为y=x+2.
(2)由直线y=x+2可知C(-2,0),
∴OC=2,
∴S△OBC=
| 1 |
| 2 |
| 1 |
| 2 |
点评:本题考查了待定系数法求函数解析式以及三角形的面积公式,正确求得k的值是本题的关键.

练习册系列答案
 全能测控期末小状元系列答案
全能测控期末小状元系列答案
相关题目
如果方程1=3-2x与关于x的方程2=
的解相同,则a的值为( )
| a-x |
| 3 |
| A、1 | ||
| B、3 | ||
| C、7 | ||
D、
|
 在截面为半圆形的水槽内装有一些水,如图.水面宽AB为6分米,如果再注入一些水后,水面AB上升1分米,水面宽变为8分米,则该水槽截面直径为( )
在截面为半圆形的水槽内装有一些水,如图.水面宽AB为6分米,如果再注入一些水后,水面AB上升1分米,水面宽变为8分米,则该水槽截面直径为( )| A、5分米 | B、6分米 |
| C、8分米 | D、10分米 |
|-3|的相反数是( )
| A、-3 | B、|-3| |
| C、3 | D、|3| |
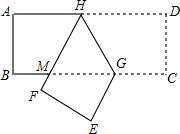 如图,已知在长方形纸条ABCD中,点G在边BC上,BG=2CG,将该纸条沿着过点G的直线翻折后,点C、D分别落在边BC下方的点E、F处,且点E、F、B在同一条直线上,折痕与边AD交于点H,HF与BG交于点M.设AB=t,那么△GHM的周长为
如图,已知在长方形纸条ABCD中,点G在边BC上,BG=2CG,将该纸条沿着过点G的直线翻折后,点C、D分别落在边BC下方的点E、F处,且点E、F、B在同一条直线上,折痕与边AD交于点H,HF与BG交于点M.设AB=t,那么△GHM的周长为
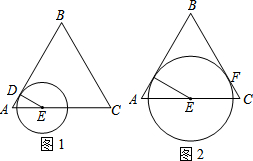 己知等边△ABC,边长为4,点D从点A出发,沿AB运动到点B,到点B停止运动.点E从A出发,沿AC的方向在直线AC上运动.点D的速度为每秒1个单位,点E的速度为每秒2个单位,它们同时出发,同时停止.以点E为圆心,DE长为半径作圆.设E点的运动时间为t秒,
己知等边△ABC,边长为4,点D从点A出发,沿AB运动到点B,到点B停止运动.点E从A出发,沿AC的方向在直线AC上运动.点D的速度为每秒1个单位,点E的速度为每秒2个单位,它们同时出发,同时停止.以点E为圆心,DE长为半径作圆.设E点的运动时间为t秒, 如图,已知AB=DB,要使△ABC≌△DBC,还要添加什么条件?添加
如图,已知AB=DB,要使△ABC≌△DBC,还要添加什么条件?添加