题目内容
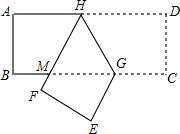 如图,已知在长方形纸条ABCD中,点G在边BC上,BG=2CG,将该纸条沿着过点G的直线翻折后,点C、D分别落在边BC下方的点E、F处,且点E、F、B在同一条直线上,折痕与边AD交于点H,HF与BG交于点M.设AB=t,那么△GHM的周长为
如图,已知在长方形纸条ABCD中,点G在边BC上,BG=2CG,将该纸条沿着过点G的直线翻折后,点C、D分别落在边BC下方的点E、F处,且点E、F、B在同一条直线上,折痕与边AD交于点H,HF与BG交于点M.设AB=t,那么△GHM的周长为考点:翻折变换(折叠问题)
专题:
分析:如图,证明BG=2GE,∠BGE=60°;证明△HMG为等边三角形;求出MG的长度,即可解决问题.
解答: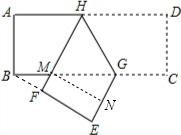 解:如图,过点M作MN⊥GE;连接BF;
解:如图,过点M作MN⊥GE;连接BF;
∵点E、F、B在同一条直线上,
∴点F在BE上;由题意得:∠E=∠D=90°,
GE=GC;∠MHG=∠DHG;
∵BG=2CG,
∴BG=2GE,∠BGE=60°;
∵四边形ABCD是矩形,
∴MH∥GE,AH∥MG,CD=AB=t.
∴∠HMG=∠BGE=60°,∠AHM=∠HMG=60°;
∴∠MHG=
=60°,
∴△HMG为等边三角形;
∵∠MFE=∠FEN=∠ENM=90°,
∴四边形MNEF为矩形,MN=FE=CD=t;
∵∠MGN=60°,
∴MG=
t,△GHM的周长=3×
t=2
t.
 解:如图,过点M作MN⊥GE;连接BF;
解:如图,过点M作MN⊥GE;连接BF;∵点E、F、B在同一条直线上,
∴点F在BE上;由题意得:∠E=∠D=90°,
GE=GC;∠MHG=∠DHG;
∵BG=2CG,
∴BG=2GE,∠BGE=60°;
∵四边形ABCD是矩形,
∴MH∥GE,AH∥MG,CD=AB=t.
∴∠HMG=∠BGE=60°,∠AHM=∠HMG=60°;
∴∠MHG=
| 180°-60° |
| 2 |
∴△HMG为等边三角形;
∵∠MFE=∠FEN=∠ENM=90°,
∴四边形MNEF为矩形,MN=FE=CD=t;
∵∠MGN=60°,
∴MG=
2
| ||
| 3 |
2
| ||
| 3 |
| 3 |
点评:该题主要考查了矩形的性质、翻折变换的性质、直角三角形的边角关系等几何知识点及其应用问题;灵活运矩形的性质、翻折变换的性质是解题的关键.

练习册系列答案
 百年学典课时学练测系列答案
百年学典课时学练测系列答案 仁爱英语同步练习册系列答案
仁爱英语同步练习册系列答案
相关题目
 有理数a、b在数轴上的位置如图所示,则a-b的结果一定是( )
有理数a、b在数轴上的位置如图所示,则a-b的结果一定是( )| A、整数 | B、分数 | C、正数 | D、负数 |
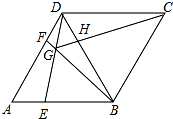 如图,在菱形ABCD中,AB=BD,点E,F分别在AB,AD上,且AE=DF.连接BF与DE相交于点G,连接CG与BD相交于点H,下列结论:①△AED≌△DFB;②S四边形BCDG=CG2;③若AF=2DF,则BG=6GF.其中正确的结论是( )
如图,在菱形ABCD中,AB=BD,点E,F分别在AB,AD上,且AE=DF.连接BF与DE相交于点G,连接CG与BD相交于点H,下列结论:①△AED≌△DFB;②S四边形BCDG=CG2;③若AF=2DF,则BG=6GF.其中正确的结论是( )| A、只有①② | B、①②③ |
| C、只有②③ | D、只有①③ |
某果园2012年水果产量为100吨,2014年水果产量为144吨,则该果园水果产量的年平均增长率为多少?若设该果园水果产量的年平均增长率为x,则根据题意可列方程为( )
| A、144(1-x)2=100 |
| B、100(1-x)2=144 |
| C、144(1+x)2=100 |
| D、100(1+x)2=144 |
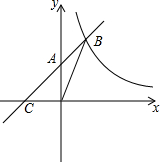 如图,一次函数y=ax+b(a≠0)图象交y轴于点A(0,2),且与反比例函数y=
如图,一次函数y=ax+b(a≠0)图象交y轴于点A(0,2),且与反比例函数y=