题目内容
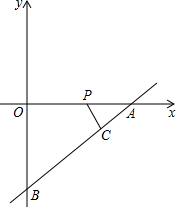
如图1,在平面直角坐标系中,直线y=-x-4分别交x轴、y轴于A,B,交双曲线y=
(x<0)于M,连OM,且S△OBM=16.
(1)求k的值.
(2)过M作MN⊥y轴于N,在直线AB上是否存在点E,使OEN的周长最小?若存在,求E点的坐标;否则说明理由;
(3)如图2,在(2)的条件下,P为双曲线上一动点,点Q为PB上一点,且AQ=AB,连MQ,NQ,求证:BQ-MQ=
NQ.

| k |
| x |
(1)求k的值.
(2)过M作MN⊥y轴于N,在直线AB上是否存在点E,使OEN的周长最小?若存在,求E点的坐标;否则说明理由;
(3)如图2,在(2)的条件下,P为双曲线上一动点,点Q为PB上一点,且AQ=AB,连MQ,NQ,求证:BQ-MQ=
| 2 |

考点:反比例函数综合题,四点共圆,线段的性质:两点之间线段最短,全等三角形的判定与性质,等腰三角形的判定与性质,圆周角定理,轴对称的性质,平行线分线段成比例
专题:压轴题
分析:(1)过M作MN⊥y轴于N,只需根据条件求出点M的坐标,就可解决问题;
(2)作点O关于直线AB的对称点O′,连接NO′,与直线AB交于点E,连接OE,根据两点之间线段最短可得此时△OEN的周长最小,然后只需依次求出点O′的坐标、直线O′N的解析式、直线O′N与直线AB的交点,就可解决问题;
(3)易证M、Q、N、B四点共圆,从而得到∠NQB=∠NMB=45°.过点N作NT⊥NQ交QB于T,如图②,则有∠NTQ=45°=∠NQB,由此可得NQ=NT,QT=
NQ,易证△QNM≌△TNB,则有QM=TB,就可得到QB-QM=QB-TB=QT=
NQ.
(2)作点O关于直线AB的对称点O′,连接NO′,与直线AB交于点E,连接OE,根据两点之间线段最短可得此时△OEN的周长最小,然后只需依次求出点O′的坐标、直线O′N的解析式、直线O′N与直线AB的交点,就可解决问题;
(3)易证M、Q、N、B四点共圆,从而得到∠NQB=∠NMB=45°.过点N作NT⊥NQ交QB于T,如图②,则有∠NTQ=45°=∠NQB,由此可得NQ=NT,QT=
| 2 |
| 2 |
解答:解:(1)过M作MN⊥y轴于N,如图①,
∵直线y=-x-4分别交x轴、y轴于A、B,
∴当x=0时,y=-4,点B(0,-4);
当y=0时,x=-4,点A(-4,0).
∵S△OBM=
OB•MN=
×4×MN=16,
∴MN=8,
∵点M在双曲线y=
(x<0)上,
∴点M的坐标为(-8,4),k=-8×4=-32;
(2)作点O关于直线AB的对称点O′,连接NO′,与直线AB交于点E,连接OE,如图①,
则有BO′=BO=4,∠O′BA=∠OBA.
根据两点之间线段最短可得此时△OEN的周长最小.
∵OA=OB,∠AOB=90°,∴∠OBA=45°,
∴∠O′BA=∠OBA=45°,
∴∠O′BO=90°,
∴点O′的坐标为(-4,-4),
设直线O′N的解析式为y=kx+4,
把O′(-4,-4)代入y=kx+4得,
∴-4k+4=-4,
∴k=2,
∴直线O′N的解析式为y=2x+4,
解
得,
,
∴点E的坐标为(-
,-
);
(3)连接AN,过点N作NT⊥NQ交QB于T,如图②,
∵∠AOB=∠MNB=90°,
∴AO∥MN,
∴
=
=1,
∴BA=AM,
∴AN=AB=AM.
∵AQ=AB,
∴AM=AQ=AN=AB,
∴M、Q、N、B四点共圆,
∴∠NQB=∠NMB.
∵MN=BN,∠MNB=90°,
∴∠NMB=∠NBM=45°,
∴∠NQB=45°.
∴∠NTQ=45°=∠NQB,
∴NQ=NT,QT=
NQ.
∵∠QNT=∠MNB=90°,
∴∠QNM=∠TNB.
在△QNM和△TNB中,
,
∴△QNM≌△TNB,
∴QM=TB,
∴QB-QM=QB-TB=QT=
NQ.

∵直线y=-x-4分别交x轴、y轴于A、B,
∴当x=0时,y=-4,点B(0,-4);
当y=0时,x=-4,点A(-4,0).
∵S△OBM=
| 1 |
| 2 |
| 1 |
| 2 |
∴MN=8,
∵点M在双曲线y=
| k |
| x |
∴点M的坐标为(-8,4),k=-8×4=-32;
(2)作点O关于直线AB的对称点O′,连接NO′,与直线AB交于点E,连接OE,如图①,
则有BO′=BO=4,∠O′BA=∠OBA.
根据两点之间线段最短可得此时△OEN的周长最小.
∵OA=OB,∠AOB=90°,∴∠OBA=45°,
∴∠O′BA=∠OBA=45°,
∴∠O′BO=90°,
∴点O′的坐标为(-4,-4),
设直线O′N的解析式为y=kx+4,
把O′(-4,-4)代入y=kx+4得,
∴-4k+4=-4,
∴k=2,
∴直线O′N的解析式为y=2x+4,
解
|
|
∴点E的坐标为(-
| 8 |
| 3 |
| 4 |
| 3 |
(3)连接AN,过点N作NT⊥NQ交QB于T,如图②,
∵∠AOB=∠MNB=90°,
∴AO∥MN,
∴
| BA |
| AM |
| BO |
| ON |
∴BA=AM,
∴AN=AB=AM.
∵AQ=AB,

∴AM=AQ=AN=AB,
∴M、Q、N、B四点共圆,
∴∠NQB=∠NMB.
∵MN=BN,∠MNB=90°,
∴∠NMB=∠NBM=45°,
∴∠NQB=45°.
∴∠NTQ=45°=∠NQB,
∴NQ=NT,QT=
| 2 |
∵∠QNT=∠MNB=90°,
∴∠QNM=∠TNB.
在△QNM和△TNB中,
|
∴△QNM≌△TNB,
∴QM=TB,
∴QB-QM=QB-TB=QT=
| 2 |
点评:本题主要考查了直线上点的坐标特征、用待定系数法求反比例函数的解析式、平行线分线段成比例、四点共圆的判定与性质、全等三角形的判定与性质、等腰三角形的判定与性质、两点之间线段最短、轴对称性等知识,综合性比较强,有一定的难度,证到∠NQB=45°并由此构造全等三角形是解决第(3)小题的关键.

练习册系列答案
 黄冈小状元满分冲刺微测验系列答案
黄冈小状元满分冲刺微测验系列答案 新辅教导学系列答案
新辅教导学系列答案 阳光同学一线名师全优好卷系列答案
阳光同学一线名师全优好卷系列答案
相关题目
下列三角形:①有两个角等于60°的三角形;②有一个角等于60°的等腰三角形;③三个外角(每个顶点处各取一个外角)都相等的三角形;④三边的高又是它的中线的三角形,其中是等边三角形的个数为( )
| A、1 | B、2 | C、3 | D、4 |
 如图,以O为圆心,OA长为半径画弧别交OM、ON于A、B两点,再分别以为A、B为圆心,以OA长为半径画弧,两弧交于点C,分别连接AC、BC,则四边形OACB一定是( )
如图,以O为圆心,OA长为半径画弧别交OM、ON于A、B两点,再分别以为A、B为圆心,以OA长为半径画弧,两弧交于点C,分别连接AC、BC,则四边形OACB一定是( )| A、梯形 | B、菱形 | C、矩形 | D、正方形 |
 如图,直线AB与直线CD交于点O,OE⊥AB,OF平分∠AOC,若∠BOD=70°.则∠EOF的度数为( )
如图,直线AB与直线CD交于点O,OE⊥AB,OF平分∠AOC,若∠BOD=70°.则∠EOF的度数为( )| A、115° | B、125° |
| C、135° | D、145° |
 如图,△ABC中,∠C=90°,AC=2,BC=1,则cosB的值是( )
如图,△ABC中,∠C=90°,AC=2,BC=1,则cosB的值是( )A、
| ||||
B、
| ||||
C、
| ||||
D、
|
 如图,直线y=
如图,直线y=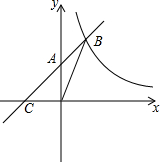 如图,一次函数y=ax+b(a≠0)图象交y轴于点A(0,2),且与反比例函数y=
如图,一次函数y=ax+b(a≠0)图象交y轴于点A(0,2),且与反比例函数y= 如图,点E在AB上,AC=AD,请你添加一个条件,使图中存在全等三角形,并给予证明.
如图,点E在AB上,AC=AD,请你添加一个条件,使图中存在全等三角形,并给予证明.