题目内容
 在截面为半圆形的水槽内装有一些水,如图.水面宽AB为6分米,如果再注入一些水后,水面AB上升1分米,水面宽变为8分米,则该水槽截面直径为( )
在截面为半圆形的水槽内装有一些水,如图.水面宽AB为6分米,如果再注入一些水后,水面AB上升1分米,水面宽变为8分米,则该水槽截面直径为( )| A、5分米 | B、6分米 |
| C、8分米 | D、10分米 |
考点:垂径定理的应用,勾股定理
专题:
分析:如图,油面AB上升1分米得到油面CD,依题意得AB=6,CD=8,过O点作AB的垂线,垂足为E,交CD于F点,连接OA,OC,由垂径定理,得AE=
AB=3,CF=
CD=4,设OE=x,则OF=x-1,在Rt△OAE中和Rt△OCF中,根据勾股定理求得OA、OC的长度,然后由OA=OC,列方程求x即可求半径OA,得出直径MN.
| 1 |
| 2 |
| 1 |
| 2 |
解答: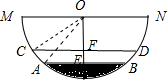 解:如图,依题意得AB=6,CD=8,过O点作AB的垂线,垂足为E,交CD于F点,连接OA,OC,
解:如图,依题意得AB=6,CD=8,过O点作AB的垂线,垂足为E,交CD于F点,连接OA,OC,
由垂径定理,得AE=
AB=3,CF=
CD=4,设OE=x,则OF=x-1,
在Rt△OAE中,OA2=AE2+OE2,
在Rt△OCF中,OC2=CF2+OF2,
∵OA=OC,
∴32+x2=42+(x-1)2,
解得x=4,
∴半径OA=
分米=5分米,
∴直径MN=2OA=10分米.
故选D.
 解:如图,依题意得AB=6,CD=8,过O点作AB的垂线,垂足为E,交CD于F点,连接OA,OC,
解:如图,依题意得AB=6,CD=8,过O点作AB的垂线,垂足为E,交CD于F点,连接OA,OC,由垂径定理,得AE=
| 1 |
| 2 |
| 1 |
| 2 |
在Rt△OAE中,OA2=AE2+OE2,
在Rt△OCF中,OC2=CF2+OF2,
∵OA=OC,
∴32+x2=42+(x-1)2,
解得x=4,
∴半径OA=
| 32+42 |
∴直径MN=2OA=10分米.
故选D.
点评:本题考查了垂径定理的运用.关键是利用垂径定理得出两个直角三角形,根据勾股定理表示半径的平方,根据半径相等列方程求解.

练习册系列答案
 备战中考寒假系列答案
备战中考寒假系列答案
相关题目
 如图,直线AB与直线CD交于点O,OE⊥AB,OF平分∠AOC,若∠BOD=70°.则∠EOF的度数为( )
如图,直线AB与直线CD交于点O,OE⊥AB,OF平分∠AOC,若∠BOD=70°.则∠EOF的度数为( )| A、115° | B、125° |
| C、135° | D、145° |
下列变形错误的是( )
| A、若a=b,则5a=5b | ||||
| B、若a=b,则3-a=3-b | ||||
| C、若am=bm,则a=b | ||||
D、若
|
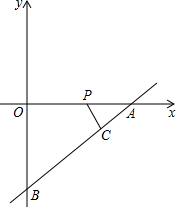 如图,直线y=
如图,直线y=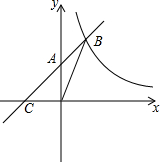 如图,一次函数y=ax+b(a≠0)图象交y轴于点A(0,2),且与反比例函数y=
如图,一次函数y=ax+b(a≠0)图象交y轴于点A(0,2),且与反比例函数y= 如图,已知在平行四边形ABCD中,点E在边BC上,射线AE交DC的延长线于点F,AB=2,BE=3EC,那么DF的长为
如图,已知在平行四边形ABCD中,点E在边BC上,射线AE交DC的延长线于点F,AB=2,BE=3EC,那么DF的长为 如图,点E在AB上,AC=AD,请你添加一个条件,使图中存在全等三角形,并给予证明.
如图,点E在AB上,AC=AD,请你添加一个条件,使图中存在全等三角形,并给予证明.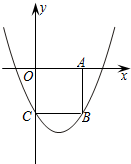 如图,在平面直角坐标系xOy中,边长为2的正方形OABC 的顶点A、C分别在x轴的正半轴和y轴的负半轴上,二次函数y=
如图,在平面直角坐标系xOy中,边长为2的正方形OABC 的顶点A、C分别在x轴的正半轴和y轴的负半轴上,二次函数y=