题目内容
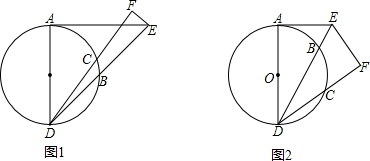
如图1,AD为⊙O的直径,B、C为⊙O上两点,点C在
上,且
=
,过A点作⊙O的切线,交DB的延长线于点E,过点E作DC的垂线,垂足为点F.
(1)求证:∠AED=∠ADF;
(2)探究BD、BE、EF三者之间数量关系,并证明;
(3)如图2,若点B在
上,其余条件不变,则BD、BE、EF三者之间又有怎样的数量关系?请证明;
(4)在(3)的条件下,当AE=3,⊙O半径为2时,求EF的长.
 |
| AB |
 |
| AB |
 |
| CD |
(1)求证:∠AED=∠ADF;
(2)探究BD、BE、EF三者之间数量关系,并证明;
(3)如图2,若点B在
 |
| AC |
(4)在(3)的条件下,当AE=3,⊙O半径为2时,求EF的长.

考点:圆的综合题
专题:综合题
分析:(1)连接AC,如图1,由
=
可得
=
,从而有∠ADF=∠DAB.然后利用切线的性质和圆周角定理即可得到∠AED=90°-∠ADB=∠DAB=∠ADF﹒
(2)连接AB、AC,过点E作EP⊥AC,交AC的延长线于点P,如图1′.易证△AEP≌△EAB,则有AP=EB.易证四边形PEFC是矩形,则有EF=CP.由
=
可得
=
,从而得到BD=AC,即可证到BD=BE-EF.
(3)连接AC、AB,过点A作AM⊥EF,交FE的延长线于点M,如图2,则有∠M=90°.易证四边形ACFM是矩形,则有AC=MF,∠CAM=90°.易证△AME≌△ABE,则有ME=BE由
=
可得
=
,从而有AC=BD,即可证到BD=BE+EF.
(4))运用勾股定理可求出DE,运用面积法可求出AB,然后运用勾股定理可求出BD,从而可求出BE,然后利用BD=BE+EF就可求出EF长.
 |
| AB |
 |
| CD |
 |
| AC |
 |
| BD |
(2)连接AB、AC,过点E作EP⊥AC,交AC的延长线于点P,如图1′.易证△AEP≌△EAB,则有AP=EB.易证四边形PEFC是矩形,则有EF=CP.由
 |
| AB |
 |
| CD |
 |
| AC |
 |
| BD |
(3)连接AC、AB,过点A作AM⊥EF,交FE的延长线于点M,如图2,则有∠M=90°.易证四边形ACFM是矩形,则有AC=MF,∠CAM=90°.易证△AME≌△ABE,则有ME=BE由
 |
| AB |
 |
| CD |
 |
| AC |
 |
| BD |
(4))运用勾股定理可求出DE,运用面积法可求出AB,然后运用勾股定理可求出BD,从而可求出BE,然后利用BD=BE+EF就可求出EF长.
解答:解:(1)连接AC,如图1.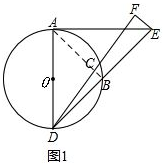
∵
=
,
∴
=
,
∴∠ADF=∠DAB.
∵AE与⊙O相切于点A,∴∠DAE=90°.
∵AD是⊙O的直径,∴∠ABD=90°,
∴∠AED=90°-∠ADB=∠DAB=∠ADF﹒
(2)BD=BE-EF.
证明:连接AB、AC,过点E作EP⊥AC,交AC的延长线于点P,如图1′.
∵AD是⊙O的直径,AE与⊙O相切于点A,
∴∠ABD=∠ACD=∠DAE=90°,
∴∠PAE=90°-∠DAC=∠ADF,
∵∠AED=∠ADF(已证),
∴∠PAE=∠AED.
在△AEP和△EAB中,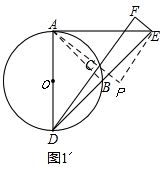
,
∴△AEP≌△EAB(AAS),
∴AP=EB.
∵EF⊥DF,∠PCF=∠ACD=90°,∠P=90°,
∴∠F=∠PCF=∠P=90°,
∴四边形PEFC是矩形,
∴EF=CP.
∵
=
,
∴
=
,
∴BD=AC,
∴BD=AC=AP-CP=BE-EF.
(3)BD=BE+EF.
证明:连接AC、AB,过点A作AM⊥EF,交FE的延长线于点M,如图2.
则有∠M=90°.
∵AD是⊙O的直径,∴∠ABD=∠ACD=90°.
∵AE与⊙O相切于点A,
∴∠DAE=90°,
∴∠BAE=90°-∠DAB=∠ADB.
∵∠F=∠ACF=∠M=90°,
∴四边形ACFM是矩形,
∴AC=MF,∠CAM=90°,
∴∠MAE=90°-∠CAE=∠DAC,
∵
=
,
∴∠ADB=∠DAC,
∴∠BAE=∠ADB=∠DAC=∠MAE.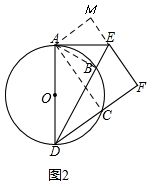
在△AME和△ABE中,
,
∴△AME≌△ABE(AAS),
∴ME=BE
∵
=
,
∴
=
,
∴AC=BD,
∴BD=AC=MF=ME+EF=BE+EF.
(4)∵∠DAE=90°,AE=3,AD=4,
∴DE=5,
∴AB=
=
=
.
∴BD=
=
,
∴BE=DE-BD=5-
=
,
∴EF=BD-BE=
-
=
.
∴EF的长为
.

∵
 |
| AB |
 |
| CD |
∴
 |
| AC |
 |
| BD |
∴∠ADF=∠DAB.
∵AE与⊙O相切于点A,∴∠DAE=90°.
∵AD是⊙O的直径,∴∠ABD=90°,
∴∠AED=90°-∠ADB=∠DAB=∠ADF﹒
(2)BD=BE-EF.
证明:连接AB、AC,过点E作EP⊥AC,交AC的延长线于点P,如图1′.
∵AD是⊙O的直径,AE与⊙O相切于点A,
∴∠ABD=∠ACD=∠DAE=90°,
∴∠PAE=90°-∠DAC=∠ADF,
∵∠AED=∠ADF(已证),
∴∠PAE=∠AED.
在△AEP和△EAB中,

|
∴△AEP≌△EAB(AAS),
∴AP=EB.
∵EF⊥DF,∠PCF=∠ACD=90°,∠P=90°,
∴∠F=∠PCF=∠P=90°,
∴四边形PEFC是矩形,
∴EF=CP.
∵
 |
| AB |
 |
| CD |
∴
 |
| AC |
 |
| BD |
∴BD=AC,
∴BD=AC=AP-CP=BE-EF.
(3)BD=BE+EF.
证明:连接AC、AB,过点A作AM⊥EF,交FE的延长线于点M,如图2.
则有∠M=90°.
∵AD是⊙O的直径,∴∠ABD=∠ACD=90°.
∵AE与⊙O相切于点A,
∴∠DAE=90°,
∴∠BAE=90°-∠DAB=∠ADB.
∵∠F=∠ACF=∠M=90°,
∴四边形ACFM是矩形,
∴AC=MF,∠CAM=90°,
∴∠MAE=90°-∠CAE=∠DAC,
∵
 |
| AB |
 |
| CD |
∴∠ADB=∠DAC,
∴∠BAE=∠ADB=∠DAC=∠MAE.

在△AME和△ABE中,
|
∴△AME≌△ABE(AAS),
∴ME=BE
∵
 |
| AB |
 |
| CD |
∴
 |
| AC |
 |
| BD |
∴AC=BD,
∴BD=AC=MF=ME+EF=BE+EF.
(4)∵∠DAE=90°,AE=3,AD=4,
∴DE=5,
∴AB=
| AD•AE |
| DE |
| 4×3 |
| 5 |
| 12 |
| 5 |
∴BD=
| AD2-AB2 |
| 16 |
| 5 |
∴BE=DE-BD=5-
| 16 |
| 5 |
| 9 |
| 5 |
∴EF=BD-BE=
| 16 |
| 5 |
| 9 |
| 5 |
| 7 |
| 5 |
∴EF的长为
| 7 |
| 5 |
点评:本题主要考查了弧与弦的关系、圆周角定理、切线的性质、全等三角形的判定与性质、矩形的判定与性质、勾股定理等知识,综合性性比较强.将两条线段的和转化成一条线段是解决第(2)小题和第(3)小题的关键.

练习册系列答案
 阶梯计算系列答案
阶梯计算系列答案
相关题目
 如图,已知AC=EF,BC=DE,点A、D、B、F在一条直线上,AD=FB,要用“边边边”证明△ABC≌△FDE,除了已知中的AC=FE,BC=DE以外,还应该有什么条件?怎样才能得到这个条件?
如图,已知AC=EF,BC=DE,点A、D、B、F在一条直线上,AD=FB,要用“边边边”证明△ABC≌△FDE,除了已知中的AC=FE,BC=DE以外,还应该有什么条件?怎样才能得到这个条件?