题目内容
已知直线m:y=kx+b过点P(1,4),且与已知直线y=-2x-1平行.
(1)求直线m的解析式;
(2)设m与x轴、y轴分别交于A、B两点,求A、B的坐标;
(3)如果直线n:y=kx+t(t>0)与m平行且交x轴于C点,求△ABC的面积s与t的函数表达式.
(1)求直线m的解析式;
(2)设m与x轴、y轴分别交于A、B两点,求A、B的坐标;
(3)如果直线n:y=kx+t(t>0)与m平行且交x轴于C点,求△ABC的面积s与t的函数表达式.
考点:两条直线相交或平行问题
专题:
分析:(1)由两条直线平行得出k=-2,再把点P(1,4)代入求得答案即可;
(2)令x=0,y=0,分别对应求得y、x的值,求得A、B的坐标;
(3)点C的位置应分在A点的左侧和右侧两种情况进行讨论.根据三角形的面积就可以求出C点的坐标.
(2)令x=0,y=0,分别对应求得y、x的值,求得A、B的坐标;
(3)点C的位置应分在A点的左侧和右侧两种情况进行讨论.根据三角形的面积就可以求出C点的坐标.
解答:解:(1)∵直线m:y=kx+b过点P(1,4),且与已知直线y=-2x-1平行.
∴k=-2,
把点P(1,4)代入y=-2x+b得b=6,
∴直线m的解析式y=-2x+6.
(2)直线m的解析式y=-2x+6.
令x=0,得出y=6,
y=0,得出x=3;
点A为(3,0)点B为(0,6).
(3)∵n∥m,
∴直线n为y=-2x+t.令y=0,解得x=
,
∴C点的坐标为(
,0).
∵t>0,
∴
>0.
∴C点在x轴的正半轴上.
当C点在A点的左侧时,S=
×(3-
)×6=9-
t;
当C点在A点的右侧时,S=
×(
-3)×6=
t-9.
∴△ABC的面积S关于t的函数表达式为S=
.
∴k=-2,
把点P(1,4)代入y=-2x+b得b=6,
∴直线m的解析式y=-2x+6.
(2)直线m的解析式y=-2x+6.
令x=0,得出y=6,
y=0,得出x=3;
点A为(3,0)点B为(0,6).
(3)∵n∥m,
∴直线n为y=-2x+t.令y=0,解得x=
| t |
| 2 |
∴C点的坐标为(
| t |
| 2 |
∵t>0,
∴
| t |
| 2 |
∴C点在x轴的正半轴上.
当C点在A点的左侧时,S=
| 1 |
| 2 |
| t |
| 2 |
| 3 |
| 2 |
当C点在A点的右侧时,S=
| 1 |
| 2 |
| t |
| 2 |
| 3 |
| 2 |
∴△ABC的面积S关于t的函数表达式为S=
|
点评:本题主要考查了待定系数法求函数的解析式,以及一次函数平行的条件,注意分类探讨思想的渗透.

练习册系列答案
相关题目
 如图所示,△ABC绕着点C顺时针旋转35°得到△A1B1C,若A1B1⊥AC,则∠A的度数是(
如图所示,△ABC绕着点C顺时针旋转35°得到△A1B1C,若A1B1⊥AC,则∠A的度数是(| A、35° | B、45° |
| C、55° | D、60° |
 如图,△ABC中,∠A=90°,A点坐标为(2,3),AB∥x轴,AC∥y轴,且 AB、AC的长是方程x2-5x+6=0的两个根,AB>AC.
如图,△ABC中,∠A=90°,A点坐标为(2,3),AB∥x轴,AC∥y轴,且 AB、AC的长是方程x2-5x+6=0的两个根,AB>AC.
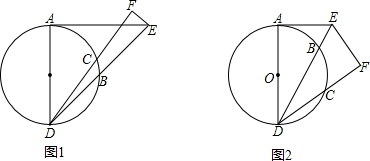
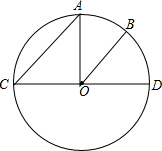 已知:如图,在⊙O中CD是直径,
已知:如图,在⊙O中CD是直径,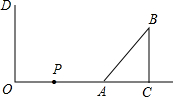 如图,在墙面OD(OD⊥OC)的右侧有一个Rt△ACB,∠ACB=90°,BC=3cm,AB=5cm,且OA=8cm,点P从点O出发,以1cm/s的速度在射线OA上运动,点Q在OD上运动,P、Q同时从O开始运动,设运动时间为t(s).
如图,在墙面OD(OD⊥OC)的右侧有一个Rt△ACB,∠ACB=90°,BC=3cm,AB=5cm,且OA=8cm,点P从点O出发,以1cm/s的速度在射线OA上运动,点Q在OD上运动,P、Q同时从O开始运动,设运动时间为t(s).