题目内容
9.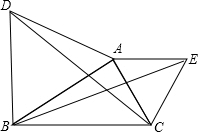 如图,△ABD,△AEC都是等边三角形,BE与DC有什么关系?你能用旋转的性质说明上述关系成立的理由吗?
如图,△ABD,△AEC都是等边三角形,BE与DC有什么关系?你能用旋转的性质说明上述关系成立的理由吗?
分析 利用△ABD、△AEC都是等边三角形,求证△DAC≌△BAE,然后即可得出BE=DC.
解答 解:BE=DC.理由:
∵△ABD、△AEC都是等边三角形,
∴AD=AB,AE=AC,∠DAB=∠CAE=60°.
∴∠DAC=∠BAC+60°,∠BAE=∠BAC+60°.
∴∠DAC=∠BAE.
在△DAC和△BAE中,
$\left\{\begin{array}{l}{AD=AB}\\{∠DAC=∠BAE}\\{AE=AC}\end{array}\right.$,
∴△DAC≌△BAE,
∴BE=DC.
点评 此题考查学生对全等三角形的判定与性质和等边三角形的性质的理解与掌握,掌握△DAC≌△BAE的条件是解题的关键.

练习册系列答案
相关题目
19.下列各组数中,不是勾股数的是( )
| A. | 13、5、12 | B. | 4、5、6 | C. | 3、4、5 | D. | 15、20、25 |
4.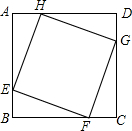 如图,正方形ABCD的边长为8,在各边上顺次截取AE=BF=CG=DH=5,则四边形EFGH的面积是( )
如图,正方形ABCD的边长为8,在各边上顺次截取AE=BF=CG=DH=5,则四边形EFGH的面积是( )
 如图,正方形ABCD的边长为8,在各边上顺次截取AE=BF=CG=DH=5,则四边形EFGH的面积是( )
如图,正方形ABCD的边长为8,在各边上顺次截取AE=BF=CG=DH=5,则四边形EFGH的面积是( )| A. | 30 | B. | 34 | C. | 36 | D. | 40 |
 如图的表格中是一些有规律的数字,观察表格填空;
如图的表格中是一些有规律的数字,观察表格填空; 如图,⊙O的直径AB=2,∠ABC=30°,C、D在圆上,则下列结论中:①∠CDB=60°;②弦AC=1;③∠ABD=30°;④OD=1,其中正确的是个数为( )
如图,⊙O的直径AB=2,∠ABC=30°,C、D在圆上,则下列结论中:①∠CDB=60°;②弦AC=1;③∠ABD=30°;④OD=1,其中正确的是个数为( )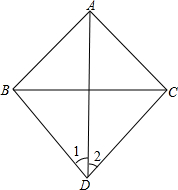 已知△ABC是等腰直角三角形,∠BAC=90°,在△ABC所在平面内有点D(点D不在△ABC内部也不在其边上),如图,连接BD、AD、CD,若∠1=∠2,求证:∠DBC=∠DCB.
已知△ABC是等腰直角三角形,∠BAC=90°,在△ABC所在平面内有点D(点D不在△ABC内部也不在其边上),如图,连接BD、AD、CD,若∠1=∠2,求证:∠DBC=∠DCB.