题目内容
14. 如图,⊙O的直径AB=2,∠ABC=30°,C、D在圆上,则下列结论中:①∠CDB=60°;②弦AC=1;③∠ABD=30°;④OD=1,其中正确的是个数为( )
如图,⊙O的直径AB=2,∠ABC=30°,C、D在圆上,则下列结论中:①∠CDB=60°;②弦AC=1;③∠ABD=30°;④OD=1,其中正确的是个数为( )| A. | 4个 | B. | 3个 | C. | 2个 | D. | 1个 |
分析 由圆周角定理可得∠ACB=90°,易得∠CAB=60°,∠CDB=∠CAB=60°,由含30°的直角三角形的性质可得AC=$\frac{1}{2}$AB=$\frac{1}{2}×2$=1,OD是圆的半径,易得OD=1,
因为△BCD不一定是等腰三角形,所以∠ABD不一定等于30°.
解答 解:∵⊙O的直径AB=2,∠ABC=30°,
∴∠ACB=90°,
∴∠CAB=60°,
∴∠CDB=∠CAB=60°,
故①正确;
在Rt△ABC中,∠ABC=30°,AB=2,
∴AC=1,
故②正确;
∵OD是圆的半径,
∴OD=1,
故④正确;
∵△BCD不一定是等腰三角形,
∴∠ABD不一定等于30°,
故③错误,
∴正确的是①②④,共3个,
故选B.
点评 本题主要考查了圆周角定理,利用圆周角定理和直角三角形的性质是解答此题的关键.

练习册系列答案
相关题目
5.-$\frac{1}{2}$的相反数是( )
| A. | 2 | B. | -2 | C. | $\frac{1}{2}$ | D. | ±$\frac{1}{2}$ |
6.二次函数y=x2+x-2的图象与x轴的交点坐标是( )
| A. | (1,0),(-2,0) | B. | (1,0),(2,0) | C. | (-1,0),(-2,0) | D. | (-1,0),(2,0) |
4.点(-2,3)在( )
| A. | x轴上 | B. | 第四象限内 | C. | 第三象限内 | D. | 第二象限内 |
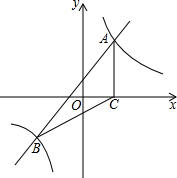 如图,一次函数y=kx+b与反比例函数y=$\frac{m}{x}$的图象交于A(2,3),B(-3,n)两点
如图,一次函数y=kx+b与反比例函数y=$\frac{m}{x}$的图象交于A(2,3),B(-3,n)两点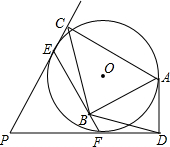 如图,PE、PF分别与⊙O相切于E、F两点,A为⊙O上不同于E、F的点,AB⊥EF于B,AC⊥PE于C,AD⊥PF于D,求证:∠ACB=∠ABD.
如图,PE、PF分别与⊙O相切于E、F两点,A为⊙O上不同于E、F的点,AB⊥EF于B,AC⊥PE于C,AD⊥PF于D,求证:∠ACB=∠ABD.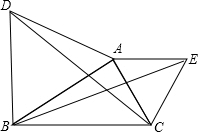 如图,△ABD,△AEC都是等边三角形,BE与DC有什么关系?你能用旋转的性质说明上述关系成立的理由吗?
如图,△ABD,△AEC都是等边三角形,BE与DC有什么关系?你能用旋转的性质说明上述关系成立的理由吗?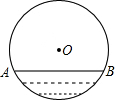 如图,水平放置一个油管其截面直径为100cm其中有油部分油面宽AB为80cm,截面上有油部分的油面高为20cm.
如图,水平放置一个油管其截面直径为100cm其中有油部分油面宽AB为80cm,截面上有油部分的油面高为20cm. 如图,G是正方形ABCD对角线AC上一点,作GE⊥AD,GF⊥AB,垂足分别为点E,F.求证:四边形AFGE与四边形ABCD相似.
如图,G是正方形ABCD对角线AC上一点,作GE⊥AD,GF⊥AB,垂足分别为点E,F.求证:四边形AFGE与四边形ABCD相似.