题目内容
19.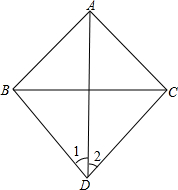 已知△ABC是等腰直角三角形,∠BAC=90°,在△ABC所在平面内有点D(点D不在△ABC内部也不在其边上),如图,连接BD、AD、CD,若∠1=∠2,求证:∠DBC=∠DCB.
已知△ABC是等腰直角三角形,∠BAC=90°,在△ABC所在平面内有点D(点D不在△ABC内部也不在其边上),如图,连接BD、AD、CD,若∠1=∠2,求证:∠DBC=∠DCB.
分析 过A作AE⊥BD于E,AF⊥CD于F,根据角平分线的性质得到AE=AF,证得Rt△AEB≌Rt△AFC,得到BE=CF,证得Rt△AED≌Rt△AFD,得到DE=DF,于是得到结论.
解答 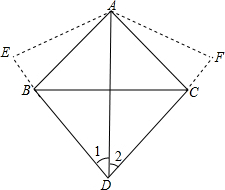 证明:过A作AE⊥BD于E,AF⊥CD于F,
证明:过A作AE⊥BD于E,AF⊥CD于F,
∵∠1=∠2,
∴AE=AF,
∵△ABC是等腰直角三角形,
∴AB=AC,
在Rt△AEB与Rt△AFC中,$\left\{\begin{array}{l}{AE=AF}\\{AB=AC}\end{array}\right.$,
∴Rt△AEB≌Rt△AFC,
∴BE=CF,
在Rt△AED与Rt△AFD中,$\left\{\begin{array}{l}{AE=AF}\\{AD=AD}\end{array}\right.$,
∴Rt△AED≌Rt△AFD,
∴DE=DF,
∴DE-BE=DF-CF,
即BD=CD,
∴∠DBC=∠DCB.
点评 本题考查了全等三角形的判定和性质,等腰直角三角形的性质,作辅助线构造全等三角形是解题的关键.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
10.如果点A的坐标满足xy=0,则点A必在( )
| A. | x轴上 | B. | y轴上 | C. | 原点 | D. | 坐标轴上 |
4.点(-2,3)在( )
| A. | x轴上 | B. | 第四象限内 | C. | 第三象限内 | D. | 第二象限内 |
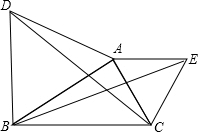 如图,△ABD,△AEC都是等边三角形,BE与DC有什么关系?你能用旋转的性质说明上述关系成立的理由吗?
如图,△ABD,△AEC都是等边三角形,BE与DC有什么关系?你能用旋转的性质说明上述关系成立的理由吗? (1)计算:$\root{3}{-8}$-|-$\sqrt{3}$|-$\sqrt{3}$($\sqrt{3}$-1)
(1)计算:$\root{3}{-8}$-|-$\sqrt{3}$|-$\sqrt{3}$($\sqrt{3}$-1)