题目内容
1.解下列方程(1)2x(x-1)=(x-1)
(2)x2-2x-2=0.
分析 (1)先移项得到2x(x-1)-(x-1)=0,然后利用因式分解法解方程;
(2)先利用配方法得到(x-1)2=3,然后利用直接开平方法解方程.
解答 解:(1)2x(x-1)-(x-1)=0,
(x-1)(2x-1)=0,
x-1=0或2x-1=0,
所以x1=1,x2=$\frac{1}{2}$;
(2)x2-2x=2,
x2-2x+1=3,
(x-1)2=3,
x-1=±$\sqrt{3}$,
所以x1=1+$\sqrt{3}$,x2=1-$\sqrt{3}$.
点评 本题考查了解一元二次方程-因式分解法:先把方程的右边化为0,再把左边通过因式分解化为两个一次因式的积的形式,那么这两个因式的值就都有可能为0,这就能得到两个一元一次方程的解,这样也就把原方程进行了降次,把解一元二次方程转化为解一元一次方程的问题了(数学转化思想).也考查了配方法解一元二次方程.

练习册系列答案
 新思维假期作业暑假吉林大学出版社系列答案
新思维假期作业暑假吉林大学出版社系列答案 蓝天教育暑假优化学习系列答案
蓝天教育暑假优化学习系列答案
相关题目
11.若4<a<5时,化简|a-4|+|a-5|=( )
| A. | 2a-9 | B. | 2a-1 | C. | 1 | D. | 9 |
16.对于抛物线y=5x2+l,有下列说法:
①抛物线与y轴的交点坐标为(1,0);
②抛物线和x轴交于两点;
③将其向右平移2个单位.再向上平移3个单位.得到的抛物线是y=5(x+2)2+4;
④当x>0时,y随x的增大而增大.
其中正确的个数为( )
①抛物线与y轴的交点坐标为(1,0);
②抛物线和x轴交于两点;
③将其向右平移2个单位.再向上平移3个单位.得到的抛物线是y=5(x+2)2+4;
④当x>0时,y随x的增大而增大.
其中正确的个数为( )
| A. | 1个 | B. | 2个 | C. | 3个 | D. | 4个 |
6.二次函数y=x2+x-2的图象与x轴的交点坐标是( )
| A. | (1,0),(-2,0) | B. | (1,0),(2,0) | C. | (-1,0),(-2,0) | D. | (-1,0),(2,0) |
10.如果点A的坐标满足xy=0,则点A必在( )
| A. | x轴上 | B. | y轴上 | C. | 原点 | D. | 坐标轴上 |
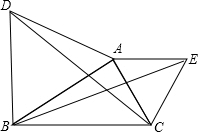 如图,△ABD,△AEC都是等边三角形,BE与DC有什么关系?你能用旋转的性质说明上述关系成立的理由吗?
如图,△ABD,△AEC都是等边三角形,BE与DC有什么关系?你能用旋转的性质说明上述关系成立的理由吗?