题目内容
19. 一个无盖长方体盒子的容积是V.
一个无盖长方体盒子的容积是V.(1)如果盒子底面是边长为a的正方形,这个盒子的表面积是多少?
(2)如果盒子底面是长为b、宽为c的长方形,这个盒子的表面积是多少?
(3)上面两种情况下,如果盒子的底面面积相等.那么两种盒子的表面积相差多少?(不计制造材料的厚度.)
分析 (1)利用长方体体积公式表示出长方体的高,进而得出其表面积;
(2)利用长方体体积公式表示出长方体的高,进而得出其表面积;
(3)利用(1),(2)中所求,进而计算得出答案.
解答 解:(1)∵一个无盖长方体盒子的容积是V,盒子地面边长为a的正方形,
∴长方体盒子的高为:h=$\frac{V}{{a}^{2}}$,
∴这个盒子的外表面积S1=a2+$\frac{V}{{a}^{2}}$×4a=a2+$\frac{4V}{a}$;
(2)∵一个无盖长方体盒子的容积是V,盒子底面是长为b,宽为c的长方形,
∴长方体盒子的高为:h=$\frac{V}{bc}$,
∴这个盒子的外表面积S2=bc+$\frac{V}{bc}$×2(b+c)=bc+$\frac{2V(b+c)}{bc}$;
(3)∵盒子的底面积相等,
∴a2=bc,
∴这两个盒子的外表面积之差:
S2-S1=bc+$\frac{2V(b+c)}{bc}$-(a2+$\frac{4V}{a}$)=a2+$\frac{2V(b+c)}{{a}^{2}}$-a2-$\frac{4V}{a}$=$\frac{2v(b+c)-4av}{{a}^{2}}$=$\frac{2v(b+c-2a)}{{a}^{2}}$.
点评 此题主要考查了几何体的表面积,列代数式,根据长方体体积得出其高度是解题关键.

练习册系列答案
 小学学习好帮手系列答案
小学学习好帮手系列答案 小学同步三练核心密卷系列答案
小学同步三练核心密卷系列答案
相关题目
9.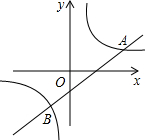 如图所示,一次函数y=kx+b和反比例函数y=$\frac{a}{x}$都经过A(2,1),B(-1,-2)两点,则不等式kx+b>$\frac{a}{x}$的解集为( )
如图所示,一次函数y=kx+b和反比例函数y=$\frac{a}{x}$都经过A(2,1),B(-1,-2)两点,则不等式kx+b>$\frac{a}{x}$的解集为( )
 如图所示,一次函数y=kx+b和反比例函数y=$\frac{a}{x}$都经过A(2,1),B(-1,-2)两点,则不等式kx+b>$\frac{a}{x}$的解集为( )
如图所示,一次函数y=kx+b和反比例函数y=$\frac{a}{x}$都经过A(2,1),B(-1,-2)两点,则不等式kx+b>$\frac{a}{x}$的解集为( )| A. | x>2 | B. | x>-1 | C. | -1<x<0或x>2 | D. | x<-1或0<x<2 |
14.一个三角形的面积是$\frac{4}{5}$平方米,其中一条边是2米,这边上的高是( )
| A. | $\frac{8}{5}$米 | B. | $\frac{4}{5}$米 | C. | $\frac{2}{5}$米 | D. | 2米 |
4.下列语句中正确的是( )
| A. | 零是自然数 | B. | 零是正数 | C. | 零是负数 | D. | 零不是整数 |
9.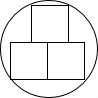 如图,三个全等的正方形内接于圆,正方形的边长为16,则圆的半径为( )
如图,三个全等的正方形内接于圆,正方形的边长为16,则圆的半径为( )
 如图,三个全等的正方形内接于圆,正方形的边长为16,则圆的半径为( )
如图,三个全等的正方形内接于圆,正方形的边长为16,则圆的半径为( )| A. | $3\sqrt{33}$ | B. | $16\sqrt{5}$ | C. | $16\sqrt{2}$ | D. | $5\sqrt{17}$ |
 如图,在Rt△ABC中,∠ACB=90°,AB=4.分别以AC,BC为直径作半圆,面积分别记为S1,S2,则S1+S2的值等于( )
如图,在Rt△ABC中,∠ACB=90°,AB=4.分别以AC,BC为直径作半圆,面积分别记为S1,S2,则S1+S2的值等于( ) 如图,点B、F、C、E在一条直线上,AB∥ED,FB=CE,AB=DE.求证:AC∥FD.
如图,点B、F、C、E在一条直线上,AB∥ED,FB=CE,AB=DE.求证:AC∥FD. 已知:如图,△ABC内接于⊙O,BD是⊙O的直径,BE切⊙O于点B,∠A=30°,则∠CBE=30度.
已知:如图,△ABC内接于⊙O,BD是⊙O的直径,BE切⊙O于点B,∠A=30°,则∠CBE=30度.