题目内容
5.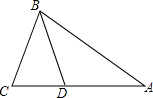 如图,在△ABC中,AB=AC,∠A=36°,BD平分∠ABC交AC于点D,若AC=2a,则AD的长是( )
如图,在△ABC中,AB=AC,∠A=36°,BD平分∠ABC交AC于点D,若AC=2a,则AD的长是( )| A. | $\frac{\sqrt{5}-1}{2}$a | B. | $\frac{\sqrt{5}+1}{2}$a | C. | ($\sqrt{5}$-1)a | D. | ($\sqrt{5}$+1)a |
分析 由在△ABC中,AB=AC,∠A=36°,BD平分∠ABC,易证得BC=BD=AD,继而证得△CBD∽△CAB,然后由相似三角形的对应边成比例,求得答案.
解答 解:∵在△ABC中,AB=AC,∠A=36°,
∴∠ABC=∠C=72°,
∵BD平分∠ABC,
∴∠CBD=∠ABD=36°,
∴∠ABD=∠A,∠C=∠BDC=72°,
∴AD=BD,BC=BD,
∴BC=BD=AD,
∴∠CBD=∠A,∠C=∠C,
∴△CBD∽△CAB,
∴CD:CB=CB:CA,
设AD=x,则CB=2a-x,
∴x2=(2a-x)•2a,
解得:x=($\sqrt{5}$-1)a.
∴AD=($\sqrt{5}$-1)a.
故选C.
点评 此题考查了等腰三角形的性质与判定以及相似三角形的判定与性质.注意证得BC=BD=AD与△CBD∽△CAB是解此题的关键.

练习册系列答案
相关题目
20.已知点A(0,4),B点在x轴上,线段AB与坐标轴围成三角形的面积为2,则B点坐标为( )
| A. | (1,0) | B. | (-1,0) | C. | (1,0)或(-1,0) | D. | (0,-1)或 (0,1) |
14.一个三角形的面积是$\frac{4}{5}$平方米,其中一条边是2米,这边上的高是( )
| A. | $\frac{8}{5}$米 | B. | $\frac{4}{5}$米 | C. | $\frac{2}{5}$米 | D. | 2米 |
15.一元二次方程2x2-7x-5=0的两根分别是x1,x2,则x1x2等于( )
| A. | $\frac{7}{2}$ | B. | $\frac{5}{2}$ | C. | -$\frac{7}{2}$ | D. | -$\frac{5}{2}$ |

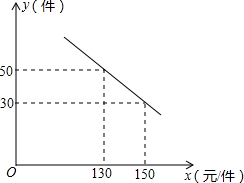 某商场购进一种每件价格为100元的新商品,在商场试销发现:销售单价x(元/件)与每天销售量y(件)之间满足如图所示的关系:
某商场购进一种每件价格为100元的新商品,在商场试销发现:销售单价x(元/件)与每天销售量y(件)之间满足如图所示的关系: 如图,在Rt△ABC中,∠ACB=90°,AB=4.分别以AC,BC为直径作半圆,面积分别记为S1,S2,则S1+S2的值等于( )
如图,在Rt△ABC中,∠ACB=90°,AB=4.分别以AC,BC为直径作半圆,面积分别记为S1,S2,则S1+S2的值等于( )