题目内容
2．
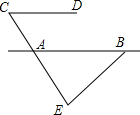如图，AB∥CD，∠C=60°，∠ABE=42°，则∠E的度数为78°．
分析 根据两直线平行同位角相等，得出∠BAE=∠C=60°，然后根据三角形内角和定理即可求得∠E的度数．
解答 解：∵AB∥CD，∠C=60°，
∴∠BAE=∠C=60°，
∵∠ABE=42°，
∴∠E=180°-60°-42°=78°，
故答案为78°．
点评 本题考查了平行线的性质和三角形内角和定理，熟练掌握性质定理是解题的关键．
练习册系列答案
相关题目
4．a为任意实数，一次函数y=ax-2a+1的图象必过一定点，此顶点的坐标为（ ）
| A． | （0，1） | B． | （1，2） | C． | （2，1） | D． | （2，0） |
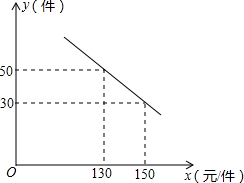某商场购进一种每件价格为100元的新商品，在商场试销发现：销售单价x（元/件）与每天销售量y（件）之间满足如图所示的关系：
如图，在Rt△ABC中，∠ACB=90°，AB=4．分别以AC，BC为直径作半圆，面积分别记为S1，S2，则S1+S2的值等于（ ）
如图，点B、F、C、E在一条直线上，AB∥ED，FB=CE，AB=DE．求证：AC∥FD．
14．一个三角形的面积是$\frac{4}{5}$平方米，其中一条边是2米，这边上的高是（ ）
| A． | $\frac{8}{5}$米 | B． | $\frac{4}{5}$米 | C． | $\frac{2}{5}$米 | D． | 2米 |
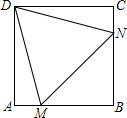如图，在正方形ABCD中，等边三角形DMN的顶点M、N分别在AB和BC上，若等边三角形DMN的边长为$2\sqrt{2}$，则正方形ABCD的边长为1+$\sqrt{3}$．