题目内容
已知:xn,
是关于x的方程anx2-4anx+4an-n=0(an>an+1)的两个实数根,xn<
,其中n为正整数,且a1=1.
(1)
-x1的值为 ;
(2)当n分别取1,2,…,2013时,相对应的有2013个方程,将这些方程的所有实数根按照从小到大的顺序排列,相邻两数的差恒为(
-x1)的值,则
-x2012= .
| x | ′ n |
| x | ′ n |
(1)
| x | ′ 1 |
(2)当n分别取1,2,…,2013时,相对应的有2013个方程,将这些方程的所有实数根按照从小到大的顺序排列,相邻两数的差恒为(
| x | ′ 1 |
| x | ′ 2013 |
考点:一元二次方程的应用,解一元二次方程-公式法,解一元二次方程-因式分解法
专题:规律型
分析:(1)当n=1时,将a1=1代入方程即可求出x1′-x1的值;
(2)表示出方程的根,根据an>an-1,得到
<
<
<…<
,当n=1,2,3,…,以及2012,2013,得到4026个公差为2的等差数列,求出所求式子即可.
(2)表示出方程的根,根据an>an-1,得到
| 1 |
| a1 |
| 2 |
| a2 |
| 3 |
| a3 |
| n |
| an |
解答:解:(1)当n=1时,将a1=1代入方程得:x2-4x+3=0,
解得:x1=1,x′1=3,
则x′1-x1=2;
故答案为:2;
(2)由求根公式得:x=2±
,
据an>an-1,得到
<
<
<…<
,
当n=1时,x1=1,x′1=3;
当n=2时,x2<x1,x′2>x′1,
当n=3时,x3<x2,x′3>x′2,
依此类推,
当n=2012时,x2012<x2011,x′2012>x′2011,
当n=2013时,x2013<x2012,x′2013>x′2012,
∴根由小到大排列为:x2013,x2012,…,x1,x′1,…,x′2013,共4026项,
∵等差且d=2,
∴x′2013=x2012+(4026-2)×2=8048.
解得:x1=1,x′1=3,
则x′1-x1=2;
故答案为:2;
(2)由求根公式得:x=2±
|
据an>an-1,得到
| 1 |
| a1 |
| 2 |
| a2 |
| 3 |
| a3 |
| n |
| an |
当n=1时,x1=1,x′1=3;
当n=2时,x2<x1,x′2>x′1,
当n=3时,x3<x2,x′3>x′2,
依此类推,
当n=2012时,x2012<x2011,x′2012>x′2011,
当n=2013时,x2013<x2012,x′2013>x′2012,
∴根由小到大排列为:x2013,x2012,…,x1,x′1,…,x′2013,共4026项,
∵等差且d=2,
∴x′2013=x2012+(4026-2)×2=8048.
点评:此题考查了一元二次方程的应用,找出题中根的规律是解本题的关键.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
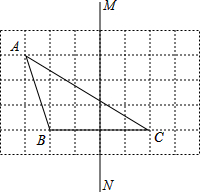 如图,在每个小正方形的边长均为l个单位长度的方格纸中,有△ABC和直线MN,点A、B、C均在小正方形的顶点上.
如图,在每个小正方形的边长均为l个单位长度的方格纸中,有△ABC和直线MN,点A、B、C均在小正方形的顶点上.
 如图,已知点A在反比例函数y=
如图,已知点A在反比例函数y=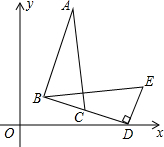 如图,在△BDE中,∠BDE=90°,BD=4
如图,在△BDE中,∠BDE=90°,BD=4 如图,在Rt△ABC中,∠C=90°,BC=9,AC=12,点D在边AC上,且CD=
如图,在Rt△ABC中,∠C=90°,BC=9,AC=12,点D在边AC上,且CD=