题目内容
 如图,已知点A在反比例函数y=
如图,已知点A在反比例函数y=| k |
| x |
| 3 |
考点:等边三角形的性质,反比例函数图象上点的坐标特征
专题:
分析:首先根据题意得出
×|2x•y|=
,进而得出xy=-
,即可得出k的值.
| 1 |
| 2 |
| 3 |
| 3 |
解答: 解:过点A作AC⊥OB于点C,
解:过点A作AC⊥OB于点C,
设A(x,y),
∵△OAB是面积为
的等边三角形,
∴
×|2x•y|=
,
∴|xy|=
,
∴xy=-
,
∴这个反比例函数的解析式是:y=-
.
故答案为:y=-
.
 解:过点A作AC⊥OB于点C,
解:过点A作AC⊥OB于点C,设A(x,y),
∵△OAB是面积为
| 3 |
∴
| 1 |
| 2 |
| 3 |
∴|xy|=
| 3 |
∴xy=-
| 3 |
∴这个反比例函数的解析式是:y=-
| ||
| x |
故答案为:y=-
| ||
| x |
点评:此题主要考查了等边三角形的性质以及三角形面积求法和反比例函数图象上点的坐标特征,得出xy=-
是解题关键.
| 3 |

练习册系列答案
 步步高口算题卡系列答案
步步高口算题卡系列答案 点睛新教材全能解读系列答案
点睛新教材全能解读系列答案 小学教材完全解读系列答案
小学教材完全解读系列答案
相关题目
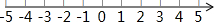 解不等式:7-x≤1-4(x-3),并把解集在所给数轴上表示出来.
解不等式:7-x≤1-4(x-3),并把解集在所给数轴上表示出来.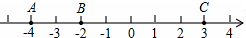
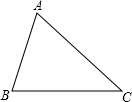 在锐角△ABC中,AB=5,BC=6,∠ACB=45°(如图),将△ABC绕点B按逆时针方向旋转得到△A′B′C′(顶点A、C分别与A′、C′对应),当点C在线段CA的延长线上时,则AC′的长度为
在锐角△ABC中,AB=5,BC=6,∠ACB=45°(如图),将△ABC绕点B按逆时针方向旋转得到△A′B′C′(顶点A、C分别与A′、C′对应),当点C在线段CA的延长线上时,则AC′的长度为 如图,要得到AB∥CD,只需要添加一个条件,这个条件可以是
如图,要得到AB∥CD,只需要添加一个条件,这个条件可以是