��Ŀ����
18���ס�����������7ʱ20�ֱַ��A��B�����г����������Ǽ��ͬһ��·������У�8ʱ40����������������ʱ���׳��ߵ�·�����ҳ��ߵ�·�̵�$\frac{4}{5}$����1����ס�����������ǰƽ��ÿСʱ����ȫ�̵ļ���֮����
��2������������������ԭ�ٶ�ǰ�����ҳ���;��ij��������һֱ��A�����������������ٶȽ�Ϊԭ�ٶȵ�$\frac{3}{5}$���׳���A����������ȫ�̵�$\frac{14}{15}$ʱ���꣨��һֱ��������B�أ����ٶȽ�Ϊԭ�ٶȵ�$\frac{3}{4}$������ҳ�����A����׳�����B�ǵ�ʱ����ͬ�������ҳ�ʲôʱ��������
���� ��1������������ǰ�׳�ƽ��ÿСʱ��ʻȫ�̵�x�����ҳ�ƽ��ÿСʱ��ʻȫ�̵�$\frac{5}{4}$x����������������ʱ$\frac{4}{3}$Сʱ�����ɵó�����x��һԪһ�η��̣��ⷽ�����x��ֵ���ɴ˼��ɵó����ۣ�
��2�����ҳ�����ʱ����ʻ��ȫ�̵�s�������������ٶ��Լ�����ͬʱ������ɵó�����s��һԪһ�η��̣��ⷽ�̼��ɵó����ۣ�
��� �⣺��1������������ǰ�׳�ƽ��ÿСʱ��ʻȫ�̵�x�����ҳ�ƽ��ÿСʱ��ʻȫ�̵�$\frac{5}{4}$x��
8ʱ40��-7ʱ20��=1ʱ20��=$\frac{4}{3}$Сʱ��
����֪�ã�$\frac{4}{3}$��x+$\frac{5}{4}$x��=1��
��ã�x=$\frac{1}{3}$��
��$\frac{5}{4}$x=$\frac{5}{12}$��
����������ǰ�׳�ƽ��ÿСʱ��ʻȫ�̵�$\frac{1}{3}$���ҳ�ƽ��ÿСʱ��ʻȫ�̵�$\frac{5}{12}$��
��2�����ҳ�����ʱ����ʻ��ȫ�̵�s��
����֪�ã�$\frac{\frac{14}{15}}{\frac{1}{3}}$+$\frac{1-\frac{14}{15}}{\frac{3}{4}��\frac{1}{3}}$=$\frac{s}{\frac{5}{12}}$+$\frac{1-s}{\frac{5}{12}��\frac{3}{5}}$��
��ã�s=$\frac{7}{12}$��
���ҳ���B����������ȫ�̵�$\frac{7}{12}$ʱ������
���� ���⿼����һԪһ�η��̵�Ӧ�ã�����Ĺؼ��ǣ���1������������ϵ�ҳ�����x��һԪһ�η��̣���2������������ϵ�ҳ�����s��һԪһ�η��̣��������ڻ����⣬�ѶȲ������������Ŀʱ������������ϵ�г������ǹؼ���

| A�� | m��0 | B�� | m��0 | C�� | m��0 | D�� | m��0 |
 ��ͼ���߳�Ϊ1��С�����������У���O��Բ���ڸ���ϣ���sin��EDB��ֵ�ǣ�������
��ͼ���߳�Ϊ1��С�����������У���O��Բ���ڸ���ϣ���sin��EDB��ֵ�ǣ�������| A�� | $\frac{1}{2}$ | B�� | $\frac{\sqrt{2}}{2}$ | C�� | $\frac{\sqrt{2}}{5}$ | D�� | $\frac{1}{5}$ |
 ��ͼ����ABC�У�AB=AC=4����C=72�㣬D��AB�е㣬��E��AC�ϣ�DE��AB����cosA��ֵΪ��������
��ͼ����ABC�У�AB=AC=4����C=72�㣬D��AB�е㣬��E��AC�ϣ�DE��AB����cosA��ֵΪ��������| A�� | $\frac{\sqrt{5}-1}{2}$ | B�� | $\frac{\sqrt{5}-1}{4}$ | C�� | $\frac{\sqrt{5}+1}{4}$ | D�� | $\frac{\sqrt{5}+1}{2}$ |

| A�� | $\frac{5}{4}$ | B�� | $\frac{4}{3}$ | C�� | 2 | D�� | 3 |

| A�� | m+4 | B�� | m+8 | C�� | 2m+4 | D�� | 2m+8 |
 ��ͼ����MON=90�㣬��A��B�ֱ�������OM��ON���˶���BEƽ�֡�NBA��BE�ķ����ӳ������BAO��ƽ���߽��ڵ�C�����C�Ķ����ǣ�������
��ͼ����MON=90�㣬��A��B�ֱ�������OM��ON���˶���BEƽ�֡�NBA��BE�ķ����ӳ������BAO��ƽ���߽��ڵ�C�����C�Ķ����ǣ�������| A�� | 30�� | B�� | 45�� | C�� | 55�� | D�� | 60�� |
 ��ǡ�ABC�У���֪��B����C��IΪ���ģ�RΪ���Բ�뾶��ADΪ��BC�ϵĸ��ߣ���K��ֱ��AD�ϣ�����AK=2R��֤������KID=$\frac{��B-��C}{2}$��
��ǡ�ABC�У���֪��B����C��IΪ���ģ�RΪ���Բ�뾶��ADΪ��BC�ϵĸ��ߣ���K��ֱ��AD�ϣ�����AK=2R��֤������KID=$\frac{��B-��C}{2}$��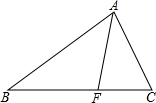 ��ͼ��ABC�У�AFƽ�֡�BAC��F��BC�ϵ�һ�㣬��BF=2CF��AC=1����AB=��������
��ͼ��ABC�У�AFƽ�֡�BAC��F��BC�ϵ�һ�㣬��BF=2CF��AC=1����AB=��������