题目内容
3. 如图,?ABCD中,BC=2AB,E为AD中点,过点C作CF⊥AB于点F,垂足F落在线段AB上,连结FE并延长与CD的延长线交于点G,则下列结论:①CE平分∠BCG;②CE=EF;③∠DEF=3∠AFE;④当AF=BF时,S△BCF=S△CEF,正确的有( )
如图,?ABCD中,BC=2AB,E为AD中点,过点C作CF⊥AB于点F,垂足F落在线段AB上,连结FE并延长与CD的延长线交于点G,则下列结论:①CE平分∠BCG;②CE=EF;③∠DEF=3∠AFE;④当AF=BF时,S△BCF=S△CEF,正确的有( )| A. | ①②③ | B. | ①②④ | C. | ①③④ | D. | ②③④ |
分析 ①正确.只要证明∠DEC=∠DCE,∠DCE=∠ECB即可解决问题.
②正确.只要证明△AEF≌△DEG,推出EF=EG,再根据直角三角形斜边中线定理即可解决问题.
③正确.只要证明∠CED=∠ECD=∠G=∠AFE,∠FEC=2∠G即可解决问题.
④错误,只要证明S△BCF=$\frac{1}{4}$S平行四边形ABCD,S△EFC=$\frac{1}{2}$S△FCG=$\frac{1}{2}$S四边形AFCD=$\frac{3}{8}$S平行四边形ABCD,推出S△BCF≠S△CEF.
解答 解:∵四边形ABCD是平行四边形,
∴AD∥CB,AB∥CD,AD=BC,AB=CD,
∴∠DEC=∠BCE,∠A=∠EDG,
∵AE=ED,AD=2CD,
∴DE=DC,
∴∠DEC=∠DCE,
∴∠DCE=∠ECB,
∴EC平分∠BCD,故①正确.
在△AEF和△DEC中,
$\left\{\begin{array}{l}{AE=ED}\\{∠AEF=∠DEG}\\{∠A=∠EDG}\end{array}\right.$,
∴△AEF≌△DEG,
∴EF=EG,
∵CF⊥AB,AB∥CD,
∴CF⊥CG,
∴∠FCG=90°,
∴CE=EF=FG,故②正确.
∵EC=EG,
∴∠G=ECG=∠AFE=∠CED,
∵∠FEC=∠G+∠ECG,
∴∠DEF=3∠AFE.故③正确,
∵AF=FB,
∴S△BCF=$\frac{1}{4}$S平行四边形ABCD,易知,S△EFC=$\frac{1}{2}$S△FCG=$\frac{1}{2}$S四边形AFCD=$\frac{3}{8}$S平行四边形ABCD,
∴S△BCF≠S△CEF,故④错误.
故选A.
点评 本题考查平行四边形的性质、全等三角形的判定和性质三角形面积等知识,解题的关键是灵活运用这些知识解决问题,属于中考常考题型.

 如图,△ABC中,AB=AC=4,∠C=72°,D是AB中点,点E在AC上,DE⊥AB,则cosA的值为( )
如图,△ABC中,AB=AC=4,∠C=72°,D是AB中点,点E在AC上,DE⊥AB,则cosA的值为( )| A. | $\frac{\sqrt{5}-1}{2}$ | B. | $\frac{\sqrt{5}-1}{4}$ | C. | $\frac{\sqrt{5}+1}{4}$ | D. | $\frac{\sqrt{5}+1}{2}$ |
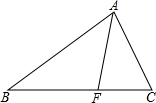 如图△ABC中,AF平分∠BAC,F是BC上的一点,且BF=2CF,AC=1,则AB=( )
如图△ABC中,AF平分∠BAC,F是BC上的一点,且BF=2CF,AC=1,则AB=( )| A. | 1 | B. | 2 | C. | 4 | D. | 6 |

 如图,∠AOB=∠COD=90°,∠AOD=132°,则∠BOC=48°.
如图,∠AOB=∠COD=90°,∠AOD=132°,则∠BOC=48°.
 如图,工人师傅在安装木质门框时,为防止变形常常像图中所示,钉上两条斜拉的木条,这样做的原理是:三角形具有稳定性.
如图,工人师傅在安装木质门框时,为防止变形常常像图中所示,钉上两条斜拉的木条,这样做的原理是:三角形具有稳定性.