题目内容
在△ABC中,∠A是∠B的2倍,∠B的补角是∠A余角的5倍,求∠C的度数.
考点:三角形内角和定理,余角和补角
专题:
分析:根据题意得出∠A与∠B的两个关系式,即可得出∠A与∠B的度数,再根据三角形的内角和定理即可得出∠C的度数.
解答:解:∵∠A是∠B的2倍,∠B的补角是∠A余角的5倍,
∴∠A=2∠B,
180-∠B=5(90-∠A),
解得∠A=60°,∠B=30°,
∴∠C=90°.
∴∠A=2∠B,
180-∠B=5(90-∠A),
解得∠A=60°,∠B=30°,
∴∠C=90°.
点评:本题考查了三角形的内角和定理、余角和补角以及二元一次方程组的解法,解题的关键是列出关于∠A与∠B的两个关系式.

练习册系列答案
 教材全解字词句篇系列答案
教材全解字词句篇系列答案
相关题目
利用数轴,可得式子|x-1|+|x-2|+|x-3|的最小值是( )
| A、1 | B、2 | C、0 | D、6 |
在Rt△ABC中,∠C=90°,则tanA•tanB等于( )
| A、0 | B、1 | C、-1 | D、不确定 |
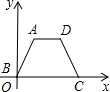 如图所示,梯形ABCD中,AB=DC=5,点A到x轴的距离是4,点C的坐标是(9,0),则梯形ABCD的面积是
如图所示,梯形ABCD中,AB=DC=5,点A到x轴的距离是4,点C的坐标是(9,0),则梯形ABCD的面积是