题目内容
以点O为圆心的三个同心圆将以OA为半径的大圆分成面积相等的四部分,且OA=4.
(1)求三个圆的半径OB,OC,OD的长.
(2)求
的值.
(1)求三个圆的半径OB,OC,OD的长.
(2)求
| OB |
| OC |
考点:算术平方根
专题:
分析:(1)先求出半径为4的圆的面积,根据已知得出方程π•OB2=
×16π,π•OC2=
×16π,π•OD2=
×16π,求出即可;
(2)代入求出即可.
| 1 |
| 4 |
| 1 |
| 2 |
| 3 |
| 4 |
(2)代入求出即可.
解答:解:(1)∵半径OA=4,
∴面积为π×42=16π,
∵以点O为圆心的三个同心圆将以OA为半径的大圆分成面积相等的四部分,
∴π•OB2=
×16π,π•OC2=
×16π,π•OD2=
×16π,
解得:OB=2,OC=2
,OD=2
;
(2)
=
=
.
∴面积为π×42=16π,
∵以点O为圆心的三个同心圆将以OA为半径的大圆分成面积相等的四部分,
∴π•OB2=
| 1 |
| 4 |
| 1 |
| 2 |
| 3 |
| 4 |
解得:OB=2,OC=2
| 2 |
| 3 |
(2)
| OB |
| OC |
| 2 | ||
2
|
| ||
| 2 |
点评:本题考查了算术平方根和圆的面积的应用,主要考查学生的计算能力.

练习册系列答案
相关题目
在二次函数y=x2+2x+4的图象中,若y随x的增大而减小,则x的取值范围是( )
| A、x>-1 | B、x<-1 |
| C、x>1 | D、x<1 |
 如图,等腰梯形ABCD中,AB=CD=5,点A到x轴的距离为4,点C的坐标为(9,0),则点D的坐标为
如图,等腰梯形ABCD中,AB=CD=5,点A到x轴的距离为4,点C的坐标为(9,0),则点D的坐标为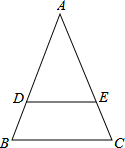 如图,已知AB=AC,DE∥BC,试证明:AD=AE.
如图,已知AB=AC,DE∥BC,试证明:AD=AE.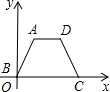 如图所示,梯形ABCD中,AB=DC=5,点A到x轴的距离是4,点C的坐标是(9,0),则梯形ABCD的面积是
如图所示,梯形ABCD中,AB=DC=5,点A到x轴的距离是4,点C的坐标是(9,0),则梯形ABCD的面积是