题目内容
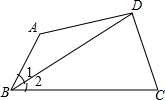 如图,BC>AB,∠1=∠2,AD=CD,探究∠BAD与∠C的关系.(用三种方法解答)
如图,BC>AB,∠1=∠2,AD=CD,探究∠BAD与∠C的关系.(用三种方法解答)考点:全等三角形的判定与性质,角平分线的性质
专题:
分析:在BC上截取BE=BA,连接DE,证△ABD≌△EBD,推出∠BAD=∠BED,根据∠BED>∠C推出即可;延长BA到E,使BE=BC,连接DE,证△EBD≌△CBD,推出∠E=∠C,根据∠BAD>∠E推出即可;根据三角形的外角性质求出即可.
解答:解:∠BAD>∠C,
理由是:方法一、
在BC上截取BE=BA,连接DE,
在△ABD和△EBD中
∴△ABD≌△EBD(SAS),
∴∠BAD=∠BED,
∵∠BED>∠C,
∴∠BAD>∠C;
方法二、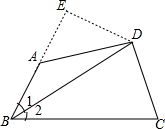
延长BA到E,使BE=BC,连接DE,
在△EBD和△CBD中
∴△EBD≌△CBD(SAS),
∴∠E=∠C,
∵∠BAD>∠E,
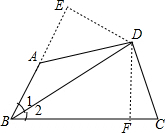 ∴∠BAD>∠C;
∴∠BAD>∠C;
方法三、
过D作DE⊥BA于E,DF⊥BC于F,
则∠E=∠DFA=90°,
∵∠BAD>∠E,∠DFB>∠C,
∴∠BAD>∠C.
理由是:方法一、

在BC上截取BE=BA,连接DE,
在△ABD和△EBD中
|
∴△ABD≌△EBD(SAS),
∴∠BAD=∠BED,
∵∠BED>∠C,
∴∠BAD>∠C;
方法二、

延长BA到E,使BE=BC,连接DE,
在△EBD和△CBD中
|
∴△EBD≌△CBD(SAS),
∴∠E=∠C,
∵∠BAD>∠E,
 ∴∠BAD>∠C;
∴∠BAD>∠C;方法三、
过D作DE⊥BA于E,DF⊥BC于F,
则∠E=∠DFA=90°,
∵∠BAD>∠E,∠DFB>∠C,
∴∠BAD>∠C.
点评:本题考查了全等三角形的性质和判定,三角形的外角性质的应用,题目比较好,难度适中.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
利用数轴,可得式子|x-1|+|x-2|+|x-3|的最小值是( )
| A、1 | B、2 | C、0 | D、6 |
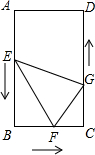 如图,在长方形ABCD中,∠A=∠B=∠C=∠D=90°,AB=DC=12cm,BC=AD=8cm,点E、F、G分别从点A、B、C三点同时出发,沿矩形的边按逆时针方向运动.点F、G的速度为2m/s,点E的速度为4m/s,设移动开始后第ts时,△EFG的面积为S(cm2).
如图,在长方形ABCD中,∠A=∠B=∠C=∠D=90°,AB=DC=12cm,BC=AD=8cm,点E、F、G分别从点A、B、C三点同时出发,沿矩形的边按逆时针方向运动.点F、G的速度为2m/s,点E的速度为4m/s,设移动开始后第ts时,△EFG的面积为S(cm2). 如图,等腰梯形ABCD中,AB=CD=5,点A到x轴的距离为4,点C的坐标为(9,0),则点D的坐标为
如图,等腰梯形ABCD中,AB=CD=5,点A到x轴的距离为4,点C的坐标为(9,0),则点D的坐标为