��Ŀ����
20����ѧ����ϣ�Сӱͬѧ��������ȫһ����������ֱ�����ǰ�ABC��DEF����̽�����������ʹ��D�����߶�AB���е㴦��ʹDF����C����ͼ1����Ȼ�����Ƶ�D˳ʱ����ת��ֱ����E����AC���ӳ�����ʱ�����������ڴ˹����У��߶�DE��AC�����ӳ��߽��ڵ�K���߶�BC��DF�ཻ�ڵ�G����ͼ2��3����
̽��1����ͼ2�У���֤����ADK�ס�BGD��
̽��2����ͼ2�У���֤��KDƽ�֡�AKG��
̽��3������ͼ3�У�KD��ƽ�֡�AKG����ƽ�֣������֤��������ƽ�֣���˵�����ɣ�
�������ϲ��������У�����AC=BC=8��KG=x����DKG�����Ϊy�������y��x�ĺ�����ϵʽ����ֱ��д��x��ȡֵ��Χ��
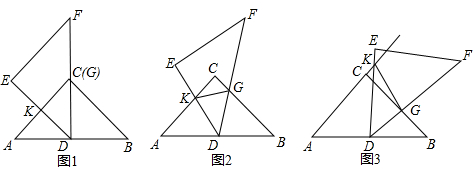
���� ̽��1�����ݡ�ABC����DEF�ǵ���ֱ�������ο�֪��KAD=��KDG=��DBG=45�㣬���������ڽǺͶ�����֪��KDA+��BDG=135�㣮��BDG+��BGD=135�㣬�ʿɵó���ADK�ס�BGD��
̽��2�����ݡ�ADK�ס�BGD��֪$\frac{AK}{BD}$=$\frac{KD}{DG}$�����ɵ�D���߶�AB���е�ó�BD=AD���ʿɵó���ADK�ס�DCK����AKD=��DKC���ɴ˿ɵó����ۣ�
̽��3����ͬ̽��1�ɵá�ADK�ס�BGD��ͬ̽��2�ɵã���ADK�ס�DGK���ʿɵó����ۣ�
�ڹ���D��DM��AC�ڵ�M��DN��KG�ڵ�N���ɢ�֪�߶�KDƽ�֡�AKG����DM=DN������AC=BC=8����D���߶�AB���е㣬��KAD=45�㣬��֪DM=DN=4�����������ε������ʽ���ɵó����ۣ�
��� �⣺̽��1��
�ߡ�KAD=��KDG=��DBG=45�㣬
���KDA+��BDG=135�㣮
�ߡ�BDG+��BGD=135�㣬
���KDA=��BGD��
���ADK�ס�BGD��
̽��2���ߡ�ADK�ס�BGD��
��$\frac{AK}{BD}$=$\frac{KD}{DG}$��
�ߵ�D���߶�AB���е㣬
��BD=AD��
��$\frac{AK}{AD}$=$\frac{KD}{DG}$��
��$\frac{AK}{KD}$=$\frac{AD}{DG}$��
�ߡ�KAD=��KDG=45�㣬
���ADK�ס�DCK��
���AKD=��DKC��
��KDƽ�֡�AKG��
̽��3����KD��ƽ�֡�AKG��
�������£�
��ͬ̽��1�ɵá�ADK�ס�BGD��
ͬ̽��2�ɵã���ADK�ס�DGK��
���AKD=��DKG��
��KD��ƽ�֡�AKG��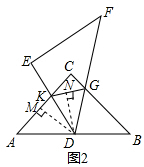
����ͼ������D��DM��AC�ڵ�M��DN��KG�ڵ�N��
�ɢ�֪�߶�KDƽ�֡�AKG��
��DM=DN��
��AC=BC=8����D���߶�AB���е㣬��KAD=45�㣬
��DM=DN=4��
��KG=x��
��S��DKG=y=$\frac{1}{2}$��4x=2x��
����ͼ3�����ͬ���ɵ�y=2x��
��KD=DGʱ����KDG�ǵ��������Σ����ADKҲ�ǵ��������Σ�AK=AD=4$\sqrt{2}$��
��CK=8-AK=8-4$\sqrt{2}$��
��CKG�ǵ���ֱ�������Σ���KG=$\sqrt{2}$CK=8��$\sqrt{2}$-1����
��E��AC���ӳ�����ʱ��
��KH��AB�ڵ�H��
��KH=z����DH=z-4$\sqrt{2}$��
��DH2+z2=64��
����z-4$\sqrt{2}$��2+z2=64��
���z=2$\sqrt{2}$+2$\sqrt{6}$��2$\sqrt{2}$-2$\sqrt{6}$����ȥ����
��AK=$\sqrt{2}$z=4+4$\sqrt{3}$��
�ߡ�ADK�ס�DGK��
��$\frac{KG}{DK}$=$\frac{DK}{AK}$����$\frac{x}{8}$=$\frac{8}{4+4\sqrt{3}}$��
���x=8��$\sqrt{3}$-1����
������ʾ��y=2x������8��$\sqrt{2}$-1����x��8��$\sqrt{3}$-1����
���� ���⿼������������ۺ��⣬�漰�����������ε��ж������ʡ�����ֱ�������ε����ʵ�֪ʶ���Ѷ����У�

| A�� | m��n | B�� | m��n | C�� | m=n | D�� | ����ȷ�� |
| A�� | -$\frac{7}{2}$ | B�� | -$\frac{1}{2}$ | C�� | -2 | D�� | -$\frac{9}{2}$ |
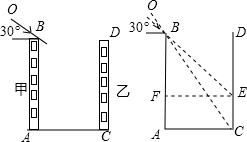 �ر���ѧ����ڼ佫����У��ò�������죮��ͼΪУ�ڵ�������ѧ¥�����ǵĸ�AB=CD=35m������֮���ˮƽ����AC=30m���ֹ��������˽��¥����¥�IJɹ��Ӱ���������̫������ˮƽ�ߵļн�Ϊ30���ʱ����EC�ĸ߶ȣ�
�ر���ѧ����ڼ佫����У��ò�������죮��ͼΪУ�ڵ�������ѧ¥�����ǵĸ�AB=CD=35m������֮���ˮƽ����AC=30m���ֹ��������˽��¥����¥�IJɹ��Ӱ���������̫������ˮƽ�ߵļн�Ϊ30���ʱ����EC�ĸ߶ȣ�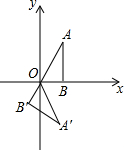 ��ͼ����B��x���ϣ���ABO=90�㣬��A=30�㣬OA=4������OAB�Ƶ�O��˳ʱ�뷽����ת120��õ���OA��B�䣬���A��������ǣ�2��-2$\sqrt{3}$����
��ͼ����B��x���ϣ���ABO=90�㣬��A=30�㣬OA=4������OAB�Ƶ�O��˳ʱ�뷽����ת120��õ���OA��B�䣬���A��������ǣ�2��-2$\sqrt{3}$����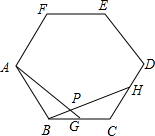 ��ͼ����G��H�ֱ�����������ABCDEF�ı�BC��CD�ϵĵ㣬��BG=CH��AG��BH�ڵ�P����1����֤����ABG�ա�BCH��
��ͼ����G��H�ֱ�����������ABCDEF�ı�BC��CD�ϵĵ㣬��BG=CH��AG��BH�ڵ�P����1����֤����ABG�ա�BCH��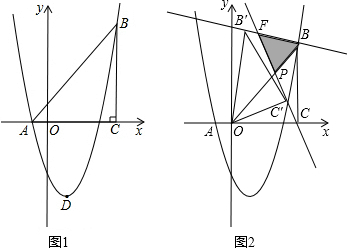
 ��ͼ��ʾ��AB��AD��BC��CD����B=3��D�����B����D�Ķ�����
��ͼ��ʾ��AB��AD��BC��CD����B=3��D�����B����D�Ķ�����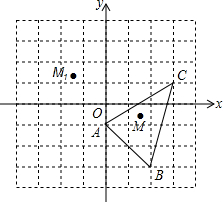 ��ͼ����ƽ��ֱ�������У�������ABC������һ��M��x��y��ƽ�ƺ�Ķ�Ӧ��ΪM1��x-3��y+2������֪��A��0��-1����B��2��-3����C��3��1����
��ͼ����ƽ��ֱ�������У�������ABC������һ��M��x��y��ƽ�ƺ�Ķ�Ӧ��ΪM1��x-3��y+2������֪��A��0��-1����B��2��-3����C��3��1����