题目内容
8.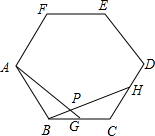 如图,点G,H分别是正六边形ABCDEF的边BC,CD上的点,且BG=CH,AG交BH于点P.(1)求证:△ABG≌△BCH;
如图,点G,H分别是正六边形ABCDEF的边BC,CD上的点,且BG=CH,AG交BH于点P.(1)求证:△ABG≌△BCH;(2)求∠APH的度数.
分析 (1)根据正六边形的性质得到AB=BC,∠ABC=∠C=120°,由三角形全等的判定定理SAS即可证出△ABG≌△BCH;
(2)由△ABG≌△BCH,得到∠BAG=∠HBC,然后根据三角形的内角和和对顶角的性质即可得到结果.
解答 (1)证明:∵在正六边形ABCDEF中,
AB=BC,∠ABC=∠C=120°,
在△ABG与△BCH中$\left\{\begin{array}{l}{AB=BC}\\{∠ABC=∠C=120°}\\{BG=CH}\end{array}\right.$,
∴△ABG≌△BCH;
(2)解:由(1)知:△ABG≌△BCH,
∴∠BAG=∠HBC,
∴∠BPG=∠ABG=120°,
∴∠APH=∠BPG=120°.
点评 本题考查了正多边形的计算及全等三角形的判定及性质,解题的关键是正确地利用正六边形中相等的元素.

练习册系列答案
相关题目
17.在某次数学测验中,某小组8名同学的成绩如下:73,81,81,81,83,85,87,89,则这组数据的中位数、众数分别为( )
| A. | 80,81 | B. | 81,89 | C. | 82,81 | D. | 73,81 |
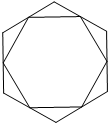 如图,顺次连接一个正六边形各边的中点,所得图形仍是正六边形.若大正六边形的面积为S1,小正六边形的面积为S2,则$\frac{{S}_{1}}{{S}_{2}}$的值是$\frac{4}{3}$.
如图,顺次连接一个正六边形各边的中点,所得图形仍是正六边形.若大正六边形的面积为S1,小正六边形的面积为S2,则$\frac{{S}_{1}}{{S}_{2}}$的值是$\frac{4}{3}$.