题目内容
5．
如图，在△ABC中，DE∥BC，AE=2，CE=3，DE=4，则BC=（ ）| A． | 6 | B． | 10 | C． | 5 | D． | 8 |
分析 由在△ABC中，DE∥BC，可得△ADE∽△ABC，然后由相似三角形的对应边成比例，求得答案．
解答 解：∵在△ABC中，DE∥BC，
∴△ADE∽△ABC，
∴$\frac{AE}{AC}$=$\frac{DE}{BC}$，
∵AE=2，CE=3，DE=4，
∴AC=AE+CE=5，
∴$\frac{2}{5}$=$\frac{4}{BC}$，
解得：BC=10．
故选B．
点评 此题考查了相似三角形的判定与性质．注意证得△ADE∽△ABC是解此题的关键．
练习册系列答案
阅读快车系列答案
相关题目
如图，将三角形ABC水平向右平移得到三角形DEF，A，D两点的距离为1，CE=2，∠A=72°，则：
如图，在△ABC中，BA=BC，以AB为直径的⊙O分别交AC，BC于点D，E，BC的延长线与⊙O的切线AF交于点F．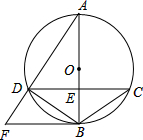
如图，已知⊙O的直径AB与弦CD相交于点E，AB⊥CD，⊙O的切线BF与弦AD的延长线相交于点F．若⊙O的半径为5，cos∠BCD=$\frac{4}{5}$，那么线段AD=8．