题目内容
19.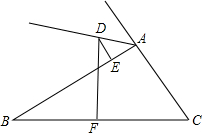 如图所示,△ABC的边BC的中垂线DF交△BAC的外角平分线AD于D,F为垂足,DE⊥AB于E,且AB>AC,试探索线段BE,AC,AE之间的数量关系并证明你的结论.
如图所示,△ABC的边BC的中垂线DF交△BAC的外角平分线AD于D,F为垂足,DE⊥AB于E,且AB>AC,试探索线段BE,AC,AE之间的数量关系并证明你的结论.
分析 结论:BE=AC+AE,连接DB、DC,作DM⊥CA于M,首先证明△ADE≌△ADM得AM=AE,再证明△BED≌△CMD得到BE=CM=CA+AM=CA+AE得证.
解答 结论: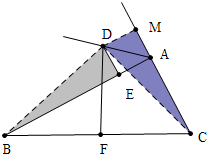 BE=AC+AE,理由如下,
BE=AC+AE,理由如下,
证明:连接DB、DC作DM⊥CA于M,
∵DA平分∠MAB,DE⊥AB,DM⊥AM,
∴DE=DM,∠DEB=∠DMC=90°,
在RT△ADE和RT△ADM中,
$\left\{\begin{array}{l}{AD=AD}\\{DE=DM}\end{array}\right.$,
∴△ADE≌△ADM,
∴AE=AM,
∵DF垂直平分BC,
∴DB=DC,
在RT△BED和RT△CMD中,
$\left\{\begin{array}{l}{DB=DC}\\{DE=DM}\end{array}\right.$,
∴△BED≌△CMD,
∴BE=CM,
∴BE=AC+AM=AC+AE.
点评 本题考查全等三角形的判定和性质、角平分线的性质、垂直平分线的性质等知识,添加辅助线构造全等三角形是解决问题的关键.

练习册系列答案
相关题目
9. 如图,下列条件中能判断L1∥L2的是( )
如图,下列条件中能判断L1∥L2的是( )
 如图,下列条件中能判断L1∥L2的是( )
如图,下列条件中能判断L1∥L2的是( )| A. | ∠1=∠2 | B. | ∠1=∠3 | C. | ∠1+∠4=180° | D. | ∠4=∠5 |
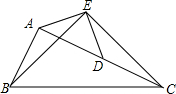 如图,在△ABC中,AC=2AB,点D是AC的中点,若BE=CE,∠ABE=∠DCE,试说明AE=DE.
如图,在△ABC中,AC=2AB,点D是AC的中点,若BE=CE,∠ABE=∠DCE,试说明AE=DE.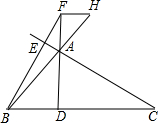 如图,在△ABC中,∠ABC=45°,∠BAC>90°,它的两条高AD,BE交于点F,过点F作FH∥BC交BA的延长线于点H,问AD,FH,CD之间有什么样的数量关系?并说明你的结论.
如图,在△ABC中,∠ABC=45°,∠BAC>90°,它的两条高AD,BE交于点F,过点F作FH∥BC交BA的延长线于点H,问AD,FH,CD之间有什么样的数量关系?并说明你的结论.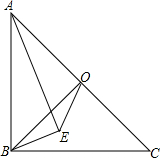 如图,在等腰Rt△ABC中,O为斜边AC的中点,连接BO,以AB为斜边向三角内部作Rt△ABE,且∠AEB=90°,连接EO.求证:
如图,在等腰Rt△ABC中,O为斜边AC的中点,连接BO,以AB为斜边向三角内部作Rt△ABE,且∠AEB=90°,连接EO.求证: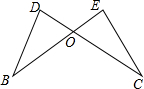 如图,BE,DC交于点O,CD=BE,∠B=∠C,求证:OB=OC.
如图,BE,DC交于点O,CD=BE,∠B=∠C,求证:OB=OC.