题目内容
14.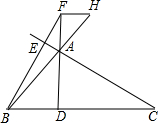 如图,在△ABC中,∠ABC=45°,∠BAC>90°,它的两条高AD,BE交于点F,过点F作FH∥BC交BA的延长线于点H,问AD,FH,CD之间有什么样的数量关系?并说明你的结论.
如图,在△ABC中,∠ABC=45°,∠BAC>90°,它的两条高AD,BE交于点F,过点F作FH∥BC交BA的延长线于点H,问AD,FH,CD之间有什么样的数量关系?并说明你的结论.
分析 结论:CD=AD+FH,先证明△ABD和△AFH都是等腰直角三角形,再证明△ADC≌△BDF得CD=DF=AD+AF=AD+FH得证.
解答 结论:CD=AD+FH,理由如下,
证明:∵ AD⊥BC,BE⊥CA,
AD⊥BC,BE⊥CA,
∴∠ADC=∠ADB=∠BDF=90°,
∵∠ABC=45°,
∴∠BAD=∠FAH=∠ABD=45°,
∴AD=BD,
∵FH∥BC,
∴∠H=∠ABD=45°,
∴∠H=∠FAH,
∴FH=AF,
∵∠C+∠EBC=90°,∠BFD+∠EBC=90°,
∴∠C=∠BFD,
在△ADC和△BDF中,
$\left\{\begin{array}{l}{∠C=∠BFD}\\{∠ADC=∠BDF}\\{AD=BD}\end{array}\right.$,
∴△ADC≌△BDF,
∴CD=DF=AD+AF=AD+FH.
点评 本题考查全等三角形的判定和性质、等腰三角形的性质,寻找全等三角形是解决问题的关键,属于中考常考题型.

练习册系列答案
相关题目
3.∠AOB是平角,从点O引射线OC,使∠AOC:∠BOC=1:5,OD是∠BOC的角平分线,则∠COD的度数是( )
| A. | 50° | B. | 65° | C. | 70° | D. | 75° |
4.某商店购进一种商品,单价为30元试销中发现这种商品每天的销售量P(件)与每件的销售价x(元)满足P=100-3x.若商店在试销期间每天销售这种商品获得200元的利润,根据题意,下面所列方程正确的是( )
| A. | (x-30)(100-3x)=200 | B. | x(100-3x)=200 | C. | (30-x)(100-3x)=200 | D. | (x-30)(3x-100)=200 |
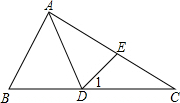 如图,在△ABC中,∠B=2∠C,AD是△ABC的角平分线,∠1=∠C,求证:AC=AB+BD.
如图,在△ABC中,∠B=2∠C,AD是△ABC的角平分线,∠1=∠C,求证:AC=AB+BD.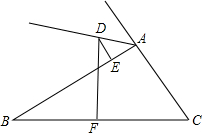 如图所示,△ABC的边BC的中垂线DF交△BAC的外角平分线AD于D,F为垂足,DE⊥AB于E,且AB>AC,试探索线段BE,AC,AE之间的数量关系并证明你的结论.
如图所示,△ABC的边BC的中垂线DF交△BAC的外角平分线AD于D,F为垂足,DE⊥AB于E,且AB>AC,试探索线段BE,AC,AE之间的数量关系并证明你的结论.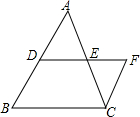 如图,点D是AB的中点,DF∥BC,CF∥AB,且DE=EF,线段BD与CF相等吗?为什么?
如图,点D是AB的中点,DF∥BC,CF∥AB,且DE=EF,线段BD与CF相等吗?为什么?