题目内容
4.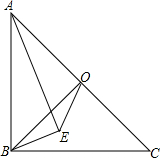 如图,在等腰Rt△ABC中,O为斜边AC的中点,连接BO,以AB为斜边向三角内部作Rt△ABE,且∠AEB=90°,连接EO.求证:
如图,在等腰Rt△ABC中,O为斜边AC的中点,连接BO,以AB为斜边向三角内部作Rt△ABE,且∠AEB=90°,连接EO.求证:(1)∠OAE=∠OBE;
(2)AE=BE+$\sqrt{2}$OE.
分析 (1)在等腰Rt△ABC中,O为斜边AC的中点,求得OB⊥AC,推出A,B,E,O四点共圆,根据圆周角定理即可得到结论;
(2)在AE上截取EF=BE,则△EFB是等腰直角三角形,于是得到$\frac{BF}{BE}=\sqrt{2}$,∠FBE=45°,根据等腰直角三角形的性质得到∠ABO=45°,推出△ABF∽△BOE,求得$\frac{AF}{OE}$=$\sqrt{2}$,根据线段的和差即可得到结论.
解答 证明:(1)在等腰Rt△ABC中,O为斜边AC的中点,
∴OB⊥AC,
∴∠AOB=90°,
∵∠AEB=90°,
∴A,B,E,O四点共圆,
∴∠OAE=∠OBE;
(2)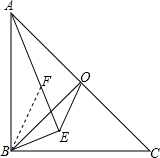 在AE上截取EF=BE,则△EFB是等腰直角三角形,
在AE上截取EF=BE,则△EFB是等腰直角三角形,
∴$\frac{BF}{BE}=\sqrt{2}$,∠FBE=45°,
∵在等腰Rt△ABC中,O为斜边AC的中点,
∴∠ABO=45°,
∴∠ABF=∠OBE,
∵$\frac{AB}{BO}=\sqrt{2}$,
∴$\frac{AB}{BO}=\frac{BF}{BE}$,
∴△ABF∽△BOE,
∴$\frac{AF}{OE}$=$\sqrt{2}$,
∴AF=$\sqrt{2}$OE,
∵AE=AF+EF,
∴AE=BE+$\sqrt{2}$OE.
点评 本题考查了相似三角形的判定和性质,等腰直角三角形的性质,正确的作出辅助线构造相似三角形是解题的关键.

练习册系列答案
相关题目
11.如果a<b,下列不等式正确的是( )
| A. | a-9>b-9 | B. | 3b<3a | C. | -2a>-2b | D. | $\frac{a}{5}$>$\frac{b}{5}$ |
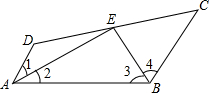 如图,已知AD∥BC,∠1=∠2,∠3=∠4,点E在DC上,试说明AD+BC=AB成立的理由.
如图,已知AD∥BC,∠1=∠2,∠3=∠4,点E在DC上,试说明AD+BC=AB成立的理由.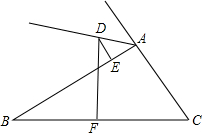 如图所示,△ABC的边BC的中垂线DF交△BAC的外角平分线AD于D,F为垂足,DE⊥AB于E,且AB>AC,试探索线段BE,AC,AE之间的数量关系并证明你的结论.
如图所示,△ABC的边BC的中垂线DF交△BAC的外角平分线AD于D,F为垂足,DE⊥AB于E,且AB>AC,试探索线段BE,AC,AE之间的数量关系并证明你的结论.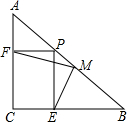 已知:如图,在△ABC中,AC=BC,∠ACB=90°,在BA上任取一点P,PE⊥BC于E,PF⊥AC于F,M是AB的中点.证明:
已知:如图,在△ABC中,AC=BC,∠ACB=90°,在BA上任取一点P,PE⊥BC于E,PF⊥AC于F,M是AB的中点.证明: 如图是半径为2的圆.
如图是半径为2的圆.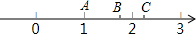 如图,数轴上A、B两点对应的实数分别为1和$\sqrt{3}$,若点A关于点B的对称点为C,则点C所对应的实数为2$\sqrt{3}$-1.
如图,数轴上A、B两点对应的实数分别为1和$\sqrt{3}$,若点A关于点B的对称点为C,则点C所对应的实数为2$\sqrt{3}$-1.