题目内容
11.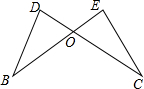 如图,BE,DC交于点O,CD=BE,∠B=∠C,求证:OB=OC.
如图,BE,DC交于点O,CD=BE,∠B=∠C,求证:OB=OC.
分析 利用两次全等进行证明,首先证明△ABE≌△ACD得AB=AC,AE=AD所以BD=EC,再证明△BOD≌△COE即可.
解答 证明:延长BD、CE交于点A.
在△ABE和△ACD中,
$\left\{\begin{array}{l}{∠A=∠A}\\{BE=CD}\\{∠B=∠E}\end{array}\right.$,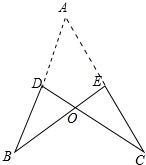
∴△ABE≌△ACD,
∴AB=AC,AE=AD,
∴BD=EC,
在△BOC和△COE中,
$\left\{\begin{array}{l}{∠B=∠C}\\{∠BOD=∠COE}\\{BD=CE}\end{array}\right.$,
∴△BOD≌△COE,
∴OB=OC.
点评 本题考查全等三角形的判定和性质,解题的关键添加辅助线构造全等三角形,两次利用全等三角形解决问题,属于中考常考题型.

练习册系列答案
 活力课时同步练习册系列答案
活力课时同步练习册系列答案
相关题目
3.∠AOB是平角,从点O引射线OC,使∠AOC:∠BOC=1:5,OD是∠BOC的角平分线,则∠COD的度数是( )
| A. | 50° | B. | 65° | C. | 70° | D. | 75° |
 如图,将△AB C向右平移5个单位长度,再向下降2个单位长度,得到△A′B′C′,请画出平移后的图形,求△ABC的面积.
如图,将△AB C向右平移5个单位长度,再向下降2个单位长度,得到△A′B′C′,请画出平移后的图形,求△ABC的面积.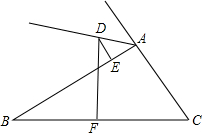 如图所示,△ABC的边BC的中垂线DF交△BAC的外角平分线AD于D,F为垂足,DE⊥AB于E,且AB>AC,试探索线段BE,AC,AE之间的数量关系并证明你的结论.
如图所示,△ABC的边BC的中垂线DF交△BAC的外角平分线AD于D,F为垂足,DE⊥AB于E,且AB>AC,试探索线段BE,AC,AE之间的数量关系并证明你的结论.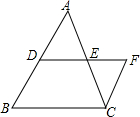 如图,点D是AB的中点,DF∥BC,CF∥AB,且DE=EF,线段BD与CF相等吗?为什么?
如图,点D是AB的中点,DF∥BC,CF∥AB,且DE=EF,线段BD与CF相等吗?为什么?