题目内容
7.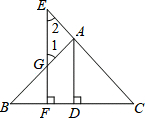 已知:如图,AD⊥BC于D,EF⊥BC于F,交AB于G,交CA延长线于E,∠1=∠2.
已知:如图,AD⊥BC于D,EF⊥BC于F,交AB于G,交CA延长线于E,∠1=∠2.求证:AD平分∠BAC.
证明:∵AD⊥BC,EF⊥BC(已知)
∴∠EFC=∠ADC=90°(垂直的定义)
∴EF∥AD(同位角相等,两直线平行)
∴∠1=∠BAD(两直线平行,内错角相等)
∠2=∠DAC(两直线平行,同位角相等)
∵∠1=∠2(已知)
∴∠DAC=∠DAB(等量代换)
即AD平分∠BAC(角平分线的定义)
分析 要证明AD平分∠BAC,只要证明∠BAD=∠CAD,而已知∠1=∠2,所以应联想这两个角分别和∠1、∠2的关系,由已知BC的两条垂线可推出EF∥AD,这时再观察这两对角的关系已不难得到结论.
解答 证明:∵AD⊥BC,EF⊥BC(已知),
∴EF∥AD(在同一平面内,垂直于同一直线的两直线平行),
∴∠1=∠BAD(两直线平行,内错角等),
∠2=∠CAD(两直线平行,同位角相等),
∵∠1=∠2(已知),
∴∠DAC=∠DAB,
即AD平分∠BAC(角平分线的定义).
故答案是:垂直的定义;同位角相等,两直线平行;∠BAD;两直线平行,同位角相等;等量代换;角平分线的定义.
点评 此题考查了角平分线的定义,平行线的性质及判定.解答此题的关键是注意平行线的性质和判定定理的综合运用.

练习册系列答案
相关题目
15.大于-2.6而不大于$\sqrt{11}$的整数共有( )
| A. | 7个 | B. | 6个 | C. | 5个 | D. | 4个 |
19.某单位招聘员工,采取笔试与面试相结合的方式进行,两项成绩的原始分满分均为100分,前六名选手的得分如下:
(1)这6名选手笔试成绩的平均数是87.5分,面试成绩的中位数是87分;
(2)现得知一号选手的综合成绩为88分,求笔试成绩和面试成绩各占的百分比;
(3)求出其余5名选手的综合成绩,并以综合成绩排序确定前两名人选.
| 序号项目 | 1 | 2 | 3 | 4 | 5 | 6 |
| 笔试成绩/分 | 85 | 92 | 84 | 90 | 84 | 80 |
| 面试成绩/分 | 90 | 88 | 86 | 90 | 80 | 85 |
(2)现得知一号选手的综合成绩为88分,求笔试成绩和面试成绩各占的百分比;
(3)求出其余5名选手的综合成绩,并以综合成绩排序确定前两名人选.
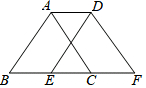 如图,将边长为2cm的等边△ABC沿边BC向右平移1cm得到△DEF,则四边形ABFD的周长为8cm.
如图,将边长为2cm的等边△ABC沿边BC向右平移1cm得到△DEF,则四边形ABFD的周长为8cm.