题目内容
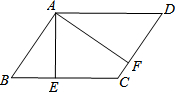 如图,在?ABCD中,AE⊥BC,AF⊥CD,E、F为垂足.若?ABCD周长为36,AE=4
如图,在?ABCD中,AE⊥BC,AF⊥CD,E、F为垂足.若?ABCD周长为36,AE=4| 3 |
| 3 |
(1)求CD;
(2)求四边形AECF的面积.
考点:平行四边形的性质,勾股定理
专题:
分析:(1)首先设CD=x,BC=y,由在?ABCD中,AE⊥BC,AF⊥CD,可得BC•AE=CD•AF,即可得方程:4
y=5
x,又由?ABCD周长为36,可得2(x+y)=36,继而求得答案;
(2)首先求得△ABE与△ADF的面积,然后由S四边形AECF=S?ABCD-S△ABE-S△ADF,求得答案.
| 3 |
| 3 |
(2)首先求得△ABE与△ADF的面积,然后由S四边形AECF=S?ABCD-S△ABE-S△ADF,求得答案.
解答:解:(1)设CD=x,BC=y,
∵在?ABCD中,AE⊥BC,AF⊥CD,
∴BC•AE=CD•AF,
∵AE=4
,AF=5
,
∴4
y=5
x,
∵?ABCD周长为36,
∴2(x+y)=36,
解得:x=8,y=10,
∴CD=8;
(2)∵四边形ABCD是平行四边形,
∴AB=CD=8,AD=BC=y=10,
∴BE=
=4,DF=
=5,
∴S△ABE=
BE•AE=8
,S△ADF=
CD•AF=
,
∴S四边形AECF=S?ABCD-S△ABE-S△ADF=8×5
-8
-
=
.
∵在?ABCD中,AE⊥BC,AF⊥CD,
∴BC•AE=CD•AF,
∵AE=4
| 3 |
| 3 |
∴4
| 3 |
| 3 |
∵?ABCD周长为36,
∴2(x+y)=36,
解得:x=8,y=10,
∴CD=8;
(2)∵四边形ABCD是平行四边形,
∴AB=CD=8,AD=BC=y=10,
∴BE=
| AB2-AE2 |
| AD2-AF2 |
∴S△ABE=
| 1 |
| 2 |
| 3 |
| 1 |
| 2 |
| 25 |
| 2 |
| 3 |
∴S四边形AECF=S?ABCD-S△ABE-S△ADF=8×5
| 3 |
| 3 |
| 25 |
| 2 |
| 3 |
| 39 |
| 2 |
| 3 |
点评:此题考查了平行四边形的性质以及勾股定理.此题难度适中,注意掌握数形结合思想与方程思想的应用.

练习册系列答案
相关题目
 如图,AB是半圆的直径,以半圆的一条弦BC(非直径)为对称轴将BC弧折叠,点D是折叠后的弧BC上一点.若∠ABC=20°,则∠CDB为
如图,AB是半圆的直径,以半圆的一条弦BC(非直径)为对称轴将BC弧折叠,点D是折叠后的弧BC上一点.若∠ABC=20°,则∠CDB为 如图,P是⊙O外一点,PA、PB分别和⊙O切于A、B两点,PA=4cm,∠P=40°,C是AB上任意一点,过点C作⊙O的切线,分别交PA、PB于点D、E,求:
如图,P是⊙O外一点,PA、PB分别和⊙O切于A、B两点,PA=4cm,∠P=40°,C是AB上任意一点,过点C作⊙O的切线,分别交PA、PB于点D、E,求: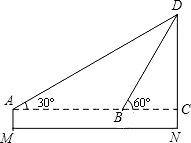 在测量操场旗杆高度的综合实践活动中某小组测绘了如下所示的示意图其中测角仪的高为1.5m,在A处测得旗杆顶部D的倾角为30°,他把测角仪向前搬了10m到达B处后,在此测得旗杆顶部D的仰角为60°,求旗杆DN的高度(结果保留小数点后一位.)
在测量操场旗杆高度的综合实践活动中某小组测绘了如下所示的示意图其中测角仪的高为1.5m,在A处测得旗杆顶部D的倾角为30°,他把测角仪向前搬了10m到达B处后,在此测得旗杆顶部D的仰角为60°,求旗杆DN的高度(结果保留小数点后一位.)