题目内容
 如图,P是⊙O外一点,PA、PB分别和⊙O切于A、B两点,PA=4cm,∠P=40°,C是AB上任意一点,过点C作⊙O的切线,分别交PA、PB于点D、E,求:
如图,P是⊙O外一点,PA、PB分别和⊙O切于A、B两点,PA=4cm,∠P=40°,C是AB上任意一点,过点C作⊙O的切线,分别交PA、PB于点D、E,求:(1)△PDE的周长;
(2)∠DOE的度数.
考点:切线的性质,切线长定理
专题:
分析:(1)直接运用切线长定理即可解决问题;
(2)如图,作辅助线,首先证明△ODA≌△ODC,得∠DOA=∠DOC,进而证明∠COE=∠BOE,问题即可解决.
(2)如图,作辅助线,首先证明△ODA≌△ODC,得∠DOA=∠DOC,进而证明∠COE=∠BOE,问题即可解决.
解答: 解:如图,连接OA、OB、OC;
解:如图,连接OA、OB、OC;
(1)∵DA、DC、EB、EC分别是⊙O的切线,
∴DA=DC,EB=EC;
∴DE=DA+EB,
∴PD+PE+DE=PD+DA+PE+BE=PA+PB,
∵PA、PB分别是⊙O的切线,
∴PA=PB=4,
∴△PDE的周长=8(cm).
(2)∵DA、DC分别是⊙O的切线,
∴OA⊥DA,OC⊥DC;
在RT△ODA与RT△ODC中,
,
∴△ODA≌△ODC(HL),
∴∠DOA=∠DOC;
同理可证:∠COE=∠BOE,
∴∠DOE=
∠AOB;
∵∠P+∠AOB=360°-90°-90°=180°,
∴∠AOB=180°-40°=140°,
∴∠DOE=70°.
 解:如图,连接OA、OB、OC;
解:如图,连接OA、OB、OC;(1)∵DA、DC、EB、EC分别是⊙O的切线,
∴DA=DC,EB=EC;
∴DE=DA+EB,
∴PD+PE+DE=PD+DA+PE+BE=PA+PB,
∵PA、PB分别是⊙O的切线,
∴PA=PB=4,
∴△PDE的周长=8(cm).
(2)∵DA、DC分别是⊙O的切线,
∴OA⊥DA,OC⊥DC;
在RT△ODA与RT△ODC中,
|
∴△ODA≌△ODC(HL),
∴∠DOA=∠DOC;
同理可证:∠COE=∠BOE,
∴∠DOE=
| 1 |
| 2 |
∵∠P+∠AOB=360°-90°-90°=180°,
∴∠AOB=180°-40°=140°,
∴∠DOE=70°.
点评:该命题以圆为载体,以考查切线的性质、切线长定理及其应用为核心构造而成;解题的关键是灵活运用有关定理来分析、判断、推理或解答.

练习册系列答案
 科学实验活动册系列答案
科学实验活动册系列答案
相关题目
关于x的方程(a-3)x2+x+2a-1=0是一元二次方程的条件是( )
| A、a≠0 | ||
| B、a≠3 | ||
C、a≠
| ||
| D、a≠-3 |
下列四个函数中,y随x的增大而减小的是( )
| A、y=4x |
| B、y=2x+5 |
| C、y=x-7 |
| D、y=-x+2 |
 如图是一次函数y=kx+b的图象,看图填空:k=
如图是一次函数y=kx+b的图象,看图填空:k=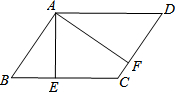 如图,在?ABCD中,AE⊥BC,AF⊥CD,E、F为垂足.若?ABCD周长为36,AE=4
如图,在?ABCD中,AE⊥BC,AF⊥CD,E、F为垂足.若?ABCD周长为36,AE=4 如图,在Rt△ABC中,∠C=90°,已知BC=6,tanA是一元二次方程5x2+2x-3=0的根,请求出AB,AC的长.
如图,在Rt△ABC中,∠C=90°,已知BC=6,tanA是一元二次方程5x2+2x-3=0的根,请求出AB,AC的长.