题目内容
已知直角三角形的两条直角边a、b是关于x的一元二次方程x2-6x+k+1=0的两个实数根,且该直角三角形的斜边c=2
,则k的值是 .
| 6 |
考点:根与系数的关系,勾股定理
专题:
分析:根据已知得出a+b=6,ab=k+1,再根据勾股定理求出k的值即可.
解答:解:∵直角三角形的两条直角边a、b是关于x的一元二次方程x2-6x+k+1=0的两个实数根,
∴a+b=6,ab=k+1,
∵a2+b2=c2,斜边c=2
,
∴(a+b)2-2ab=24,
∴62-2(k+1)=24,
∴k=5;
故答案为:5.
∴a+b=6,ab=k+1,
∵a2+b2=c2,斜边c=2
| 6 |
∴(a+b)2-2ab=24,
∴62-2(k+1)=24,
∴k=5;
故答案为:5.
点评:此题考查了根与系数的关系,将根与系数的关系与代数式变形相结合解题是一种经常使用的解题方法.

练习册系列答案
相关题目
下列四个函数中,y随x的增大而减小的是( )
| A、y=4x |
| B、y=2x+5 |
| C、y=x-7 |
| D、y=-x+2 |
 如图是一次函数y=kx+b的图象,看图填空:k=
如图是一次函数y=kx+b的图象,看图填空:k=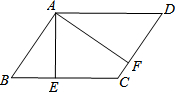 如图,在?ABCD中,AE⊥BC,AF⊥CD,E、F为垂足.若?ABCD周长为36,AE=4
如图,在?ABCD中,AE⊥BC,AF⊥CD,E、F为垂足.若?ABCD周长为36,AE=4 如图,AB是⊙O的直径,弦CD⊥AB,垂足为F,点E在⊙O上,∠ABD与∠AEC相等吗?为什么?
如图,AB是⊙O的直径,弦CD⊥AB,垂足为F,点E在⊙O上,∠ABD与∠AEC相等吗?为什么?