题目内容
5.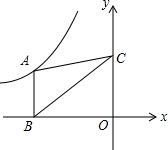 如图,在平面直角坐标系中,点A在函数y=$\frac{k}{x}$(k<0,x<0)的图象上,过点A作AB∥y轴交x轴于点B,点C在y轴上,连结AC、BC.若△ABC的面积是3,则k=-6.
如图,在平面直角坐标系中,点A在函数y=$\frac{k}{x}$(k<0,x<0)的图象上,过点A作AB∥y轴交x轴于点B,点C在y轴上,连结AC、BC.若△ABC的面积是3,则k=-6.
分析 设点A的坐标为(m,$\frac{k}{m}$),由点A的坐标结合△ABC的面积即可得出k的值.
解答 解:设点A的坐标为(m,$\frac{k}{m}$).
∵S△ABC=$\frac{1}{2}$AB•OB=$\frac{k}{m}$×(-m)=3,
∴k=-6.
故答案为:-6.
点评 本题考查了反比例函数图象上点的坐标特征,解题的关键是求出点A的横纵坐标之积.本题属于基础题,难度不大,解决该题型题目时,用点A的坐标来表示三角形的面积是关键.

练习册系列答案
相关题目
13.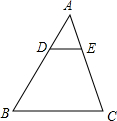 如图,在△ABC中,DE∥BC,$\frac{AD}{DB}$=$\frac{1}{2}$,则下列结论中正确的是( )
如图,在△ABC中,DE∥BC,$\frac{AD}{DB}$=$\frac{1}{2}$,则下列结论中正确的是( )
 如图,在△ABC中,DE∥BC,$\frac{AD}{DB}$=$\frac{1}{2}$,则下列结论中正确的是( )
如图,在△ABC中,DE∥BC,$\frac{AD}{DB}$=$\frac{1}{2}$,则下列结论中正确的是( )| A. | $\frac{AE}{AC}$=$\frac{1}{2}$ | B. | $\frac{DE}{BC}$=$\frac{1}{2}$ | ||
| C. | $\frac{△ADE的周长}{△ABC的周长}$=$\frac{1}{3}$ | D. | $\frac{△ADE的面积}{△ABC的面积}$=$\frac{1}{4}$ |
15.为了解七年级学生上学期参加社会实践活动的情况,随机抽查A市七年级部分学生参加社会实践活动天数,并根据抽查结果制作了如下不完整的频数分布表和条形统计图.
A市七年级部分学生参加社会实践活动天数的频数分布表
A市七年级部分学生参加社会实践活动天数的条形统计图
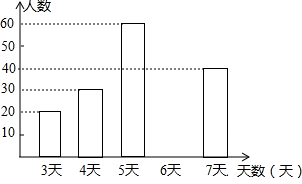
根据以上信息,解答下列问题;
(1)求出频数分布表中a的值,并补全条形统计图.
(2)A市有七年级学生20000人,请你估计该市七年级学生参加社会实践活动不少于5天的人数.
A市七年级部分学生参加社会实践活动天数的频数分布表
| 天数 | 频数 | 频率 |
| 3 | 20 | 0.10 |
| 4 | 30 | 0.15 |
| 5 | 60 | 0.30 |
| 6 | a | 0.25 |
| 7 | 40 | 0.20 |

根据以上信息,解答下列问题;
(1)求出频数分布表中a的值,并补全条形统计图.
(2)A市有七年级学生20000人,请你估计该市七年级学生参加社会实践活动不少于5天的人数.
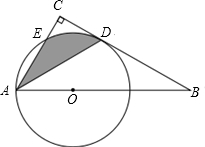 如图,Rt△ABC中,∠BAC=60°,点O为Rt△ABC斜边AB上的一点,以OA为半径的⊙O与BC切于点D,与AC交于点E,连接AD.
如图,Rt△ABC中,∠BAC=60°,点O为Rt△ABC斜边AB上的一点,以OA为半径的⊙O与BC切于点D,与AC交于点E,连接AD.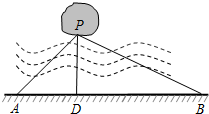 如图,宁波市共湖中有一小岛,湖边有一条笔直的观光小道AB,现决定从小岛架一座与观光小道垂直的小桥PD,在小道上测得如下数据:AB=60米,∠PAB=45°,∠PBA=30°.请帮助小张求出小桥PD的长.($\sqrt{2}$≈1.414,$\sqrt{3}$≈1.732,结果精确到0.1米)
如图,宁波市共湖中有一小岛,湖边有一条笔直的观光小道AB,现决定从小岛架一座与观光小道垂直的小桥PD,在小道上测得如下数据:AB=60米,∠PAB=45°,∠PBA=30°.请帮助小张求出小桥PD的长.($\sqrt{2}$≈1.414,$\sqrt{3}$≈1.732,结果精确到0.1米)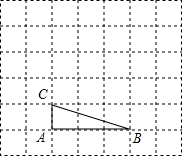 如图,将△ABC放在每个小正方形的边长为1的网格中,点A,点B,点C均落在格点上.
如图,将△ABC放在每个小正方形的边长为1的网格中,点A,点B,点C均落在格点上.