题目内容
13.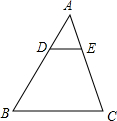 如图,在△ABC中,DE∥BC,$\frac{AD}{DB}$=$\frac{1}{2}$,则下列结论中正确的是( )
如图,在△ABC中,DE∥BC,$\frac{AD}{DB}$=$\frac{1}{2}$,则下列结论中正确的是( )| A. | $\frac{AE}{AC}$=$\frac{1}{2}$ | B. | $\frac{DE}{BC}$=$\frac{1}{2}$ | ||
| C. | $\frac{△ADE的周长}{△ABC的周长}$=$\frac{1}{3}$ | D. | $\frac{△ADE的面积}{△ABC的面积}$=$\frac{1}{4}$ |
分析 根据△ABC中DE∥BC可以得到△ADE∽△ABC,再根据AD:DB=1:2可以得到AD:AB=1:3,从而得到两相似三角形的相似比为1:3,利用周长的比等于相似比,面积的比等于相似比的平方可以得到答案.
解答 解:∵DE∥BC,
∴△ADE∽△ABC,
∵AD:DB=1:2
∴AD:AB=1:3,
∴两相似三角形的相似比为1:3,
∵周长的比等于相似比,面积的比等于相似比的平方,
∴C正确.
故选C.
点评 本题考查了相似三角形的判定及性质,解题的关键是了解相似三角形周长的比等于对应边的比.

练习册系列答案
相关题目
8.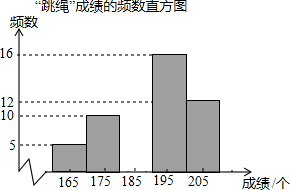 某校为了解九年级学生的身体素质情况,从全校500名九年级学生中随机抽取了部分学生进行体育测试,其中“跳绳”成绩制成如下频数表和频数直方图:
某校为了解九年级学生的身体素质情况,从全校500名九年级学生中随机抽取了部分学生进行体育测试,其中“跳绳”成绩制成如下频数表和频数直方图:
“跳绳”成绩的频数表
根据图表解决下列问题:
(1)本次抽样调查的样本容量是50,频数表中,a=0.2,b=7c=0.32;
(2)数据分组的组距是10,本次调查的个体是被抽到的每名九年级学生的跳绳成绩;
(3)补全频数直方图;
(4)“跳绳”数在180以上,则此项成绩可得满分,请估计全校九年级有多少学生在此项成绩中获满分.
 某校为了解九年级学生的身体素质情况,从全校500名九年级学生中随机抽取了部分学生进行体育测试,其中“跳绳”成绩制成如下频数表和频数直方图:
某校为了解九年级学生的身体素质情况,从全校500名九年级学生中随机抽取了部分学生进行体育测试,其中“跳绳”成绩制成如下频数表和频数直方图:“跳绳”成绩的频数表
| 组别 | 组中值(个) | 频数 | 频率 |
| A | 165 | 5 | 0.1 |
| B | 175 | 10 | a |
| C | 185 | b | 0.14 |
| D | 195 | 16 | c |
| E | 205 | 12 | 0.24 |
(1)本次抽样调查的样本容量是50,频数表中,a=0.2,b=7c=0.32;
(2)数据分组的组距是10,本次调查的个体是被抽到的每名九年级学生的跳绳成绩;
(3)补全频数直方图;
(4)“跳绳”数在180以上,则此项成绩可得满分,请估计全校九年级有多少学生在此项成绩中获满分.
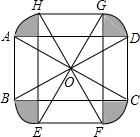 如图,将矩形ABCD绕对角线的交点0逆时针旋转90°得到矩形EFGH,已知AB=2,BC=2$\sqrt{3}$,则由旋转得到的阴影部分的面积为$\frac{4}{3}$π+4-4$\sqrt{3}$.
如图,将矩形ABCD绕对角线的交点0逆时针旋转90°得到矩形EFGH,已知AB=2,BC=2$\sqrt{3}$,则由旋转得到的阴影部分的面积为$\frac{4}{3}$π+4-4$\sqrt{3}$. 我国明代数学家程大位的名著《直指算法统宗》里有一道著名算题:
我国明代数学家程大位的名著《直指算法统宗》里有一道著名算题: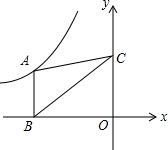 如图,在平面直角坐标系中,点A在函数y=$\frac{k}{x}$(k<0,x<0)的图象上,过点A作AB∥y轴交x轴于点B,点C在y轴上,连结AC、BC.若△ABC的面积是3,则k=-6.
如图,在平面直角坐标系中,点A在函数y=$\frac{k}{x}$(k<0,x<0)的图象上,过点A作AB∥y轴交x轴于点B,点C在y轴上,连结AC、BC.若△ABC的面积是3,则k=-6.