题目内容
17.(1)计算:|1-$\sqrt{3}$|+($\frac{1}{2}$)-1-2cos30°.(2)化简:$\frac{2a}{{a}^{2}-4}$-$\frac{1}{a-2}$.
分析 (1)本题涉及绝对值、负整数指数幂、特殊角的三角函数值、二次根式化简4个考点.在计算时,需要针对每个考点分别进行计算,然后根据实数的运算法则求得计算结果;
(2)异分母分式加减法法则:把分母不相同的几个分式化成分母相同的分式,叫做通分,经过通分,异分母分式的加减就转化为同分母分式的加减.
解答 解:(1)|1-$\sqrt{3}$|+($\frac{1}{2}$)-1-2cos30°
=$\sqrt{3}$-1+2-2×$\frac{\sqrt{3}}{2}$
=$\sqrt{3}$-1+2-$\sqrt{3}$
=1;
(2)$\frac{2a}{{a}^{2}-4}$-$\frac{1}{a-2}$
=$\frac{2a}{(a+2)(a-2)}$-$\frac{a+2}{(a+2)(a-2)}$
=$\frac{a-2}{(a+2)(a-2)}$
=$\frac{1}{a+2}$.
点评 本题主要考查了实数的综合运算能力,是各地中考题中常见的计算题型.解决此类题目的关键是熟练掌握绝对值、负整数指数幂、特殊角的三角函数值、二次根式等考点的运算.同时考查了分式的加减法,注意:①分式的通分必须注意整个分子和整个分母,分母是多项式时,必须先分解因式,分子是多项式时,要把分母所乘的相同式子与这个多项式相乘,而不能只同其中某一项相乘.②通分是和约分是相反的一种变换.约分是把分子和分母的所有公因式约去,将分式化为较简单的形式;通分是分别把每一个分式的分子分母同乘以相同的因式,使几个较简单的分式变成分母相同的较复杂的形式.约分是对一个分式而言的;通分则是对两个或两个以上的分式来说的.

练习册系列答案
 阳光同学一线名师全优好卷系列答案
阳光同学一线名师全优好卷系列答案
相关题目
8.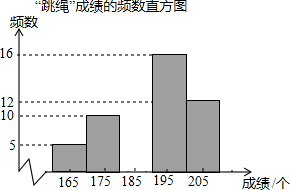 某校为了解九年级学生的身体素质情况,从全校500名九年级学生中随机抽取了部分学生进行体育测试,其中“跳绳”成绩制成如下频数表和频数直方图:
某校为了解九年级学生的身体素质情况,从全校500名九年级学生中随机抽取了部分学生进行体育测试,其中“跳绳”成绩制成如下频数表和频数直方图:
“跳绳”成绩的频数表
根据图表解决下列问题:
(1)本次抽样调查的样本容量是50,频数表中,a=0.2,b=7c=0.32;
(2)数据分组的组距是10,本次调查的个体是被抽到的每名九年级学生的跳绳成绩;
(3)补全频数直方图;
(4)“跳绳”数在180以上,则此项成绩可得满分,请估计全校九年级有多少学生在此项成绩中获满分.
 某校为了解九年级学生的身体素质情况,从全校500名九年级学生中随机抽取了部分学生进行体育测试,其中“跳绳”成绩制成如下频数表和频数直方图:
某校为了解九年级学生的身体素质情况,从全校500名九年级学生中随机抽取了部分学生进行体育测试,其中“跳绳”成绩制成如下频数表和频数直方图:“跳绳”成绩的频数表
| 组别 | 组中值(个) | 频数 | 频率 |
| A | 165 | 5 | 0.1 |
| B | 175 | 10 | a |
| C | 185 | b | 0.14 |
| D | 195 | 16 | c |
| E | 205 | 12 | 0.24 |
(1)本次抽样调查的样本容量是50,频数表中,a=0.2,b=7c=0.32;
(2)数据分组的组距是10,本次调查的个体是被抽到的每名九年级学生的跳绳成绩;
(3)补全频数直方图;
(4)“跳绳”数在180以上,则此项成绩可得满分,请估计全校九年级有多少学生在此项成绩中获满分.
 如图,在平行四边形ABCD中,AB=3,AD=4,∠ABC=60°,过BC的中点E作EF⊥AB于点F,交DC的延长线于点G,则DE=$\sqrt{19}$.
如图,在平行四边形ABCD中,AB=3,AD=4,∠ABC=60°,过BC的中点E作EF⊥AB于点F,交DC的延长线于点G,则DE=$\sqrt{19}$.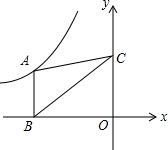 如图,在平面直角坐标系中,点A在函数y=$\frac{k}{x}$(k<0,x<0)的图象上,过点A作AB∥y轴交x轴于点B,点C在y轴上,连结AC、BC.若△ABC的面积是3,则k=-6.
如图,在平面直角坐标系中,点A在函数y=$\frac{k}{x}$(k<0,x<0)的图象上,过点A作AB∥y轴交x轴于点B,点C在y轴上,连结AC、BC.若△ABC的面积是3,则k=-6.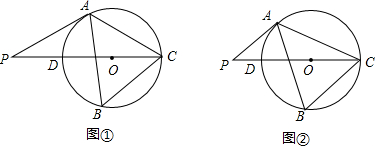
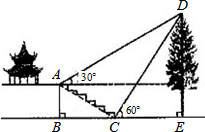 如图,某校综合实践活动小组的同学欲测量公园内一棵树DE的高度,他们在这棵树正前方一座楼亭前的台阶上A点处测得树顶端D的仰角为30°,朝着这棵树的方向走到台阶下的点C处,测得树顶端D的仰角为60°.已知A点的高度AB为2m,台阶AC的坡度为1:$\sqrt{3}$,且B,C,E三点在同一条直线上.请根据以上条件求出树DE的高度(测倾器的高度忽略不计).
如图,某校综合实践活动小组的同学欲测量公园内一棵树DE的高度,他们在这棵树正前方一座楼亭前的台阶上A点处测得树顶端D的仰角为30°,朝着这棵树的方向走到台阶下的点C处,测得树顶端D的仰角为60°.已知A点的高度AB为2m,台阶AC的坡度为1:$\sqrt{3}$,且B,C,E三点在同一条直线上.请根据以上条件求出树DE的高度(测倾器的高度忽略不计).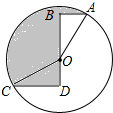 如图,⊙O的半径为2,点A、C在⊙O上,线段BD经过圆心O,∠ABD=∠CDB=90°,AB=1,CD=$\sqrt{3}$,则图中阴影部分的面积为$\frac{5}{3}$π.
如图,⊙O的半径为2,点A、C在⊙O上,线段BD经过圆心O,∠ABD=∠CDB=90°,AB=1,CD=$\sqrt{3}$,则图中阴影部分的面积为$\frac{5}{3}$π.