Question

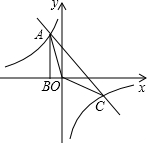如图，Rt△ABO的顶点A是双曲线y=

k

x

与直线y=-x-（k+1）在第二象限的交点，AB⊥x轴于点B，且S_△AOB=

3

2

．在第四象限的双曲线上是否存在点P使△POC的面积等于△AOC？若存在，请求出点P坐标；若不存在，说明理由．

Answer 1

考点：反比例函数与一次函数的交点问题

专题：

分析：根据反比例函数k的几何意义可求得k=-3，则反比例函数的解析式为y=-

3

x

，一次函数的解析式为y=-x+2，再解两解析式所组成的方程组确定点A、C的坐标分别是（-1，3），（3，-1），利用S_△AOC=S_△ADO+S_△CDO进行计算，求出S_△AOC=4．作PE⊥x轴于E，CF⊥x轴于F，设P点坐标为（x，y），由于S_△POC+S_△OCF=S_梯形CFEP+S_△POE，而S_△OCF=S_△POE，则S_△POC=S_梯形CFEP．然后分点P在C的左侧与点P在C的右侧两种情况，根据S_梯形CFEP=4列出方程，解方程即可．

解答：解：∵S_△AOB=

3

2

，
∴

1

2

|k|=

3

2

，
而反比例函数图象在第二、四象限，即k＜0，
∴k=-3，
∴反比例函数的解析式为y=-

3

x

，一次函数的解析式为y=-x+2，
根据题意得：

y=-x+2 y=- 3 x

，解得

x1=-1 y1=3

，

x2=3 y2=-1

，
∴交点A为（-1，3），C为（3，-1），
对于y=-x+2，令x=0，解得y=2，则直线y=-x+2与y轴的交点D的坐标为（0，2），
∴S_△AOC=S_△ADO+S_△CDO=

1

2

×2×1+

1

2

×2×3=4．
作PE⊥x轴于E，CF⊥x轴于F，设P点坐标为（x，y），
∵S_△POC+S_△OCF=S_梯形CFEP+S_△POE，
而S_△OCF=S_△POE，
∴S_△POC=S_梯形CFEP．
①当点P在C的左侧时，

1

2

（-y+1）（3-x）=4，
∵y=-

3

x

，
∴x²+8x-9=0，
解得x₁=-9（舍去），x₂=1，
当x=1时，y=-3，
∴P点坐标为（1，-3）；
②当点P在C的右侧时，同理，求得P点坐标为（9，-

1

3

）．
综上所述，在第四象限的双曲线上存在点P使△POC的面积等于△AOC，此时点P的坐标为（1，-3）或（9，-

1

3

）．

点评：本题考查了反比例函数与一次函数的交点问题：反比例函数与一次函数的图象的交点坐标满足两个函数的解析式．也考查了三角形面积公式．