题目内容
 已知,如图:A、E、F、B在一条直线上,AE=BF,∠C=∠D,CF∥DE,
已知,如图:A、E、F、B在一条直线上,AE=BF,∠C=∠D,CF∥DE,求证:AC∥BD.
考点:全等三角形的判定与性质
专题:证明题
分析:求出AF=BE,根据平行线性质求出∠AFC=∠BED,根据AAS推出△ACF≌△BDE,再根据平行线的判定得出结论即可.
解答:证明:∵AE=BF,
∴AE+EF=BF+EF,
∴AF=BE,
∵CF∥DE,
∴∠AFC=∠BEDB,
在△ACF和△BDE中,
,
∴△ACF≌△BDE(AAS),
∴∠A=∠B,
∴AC∥BD.
∴AE+EF=BF+EF,
∴AF=BE,
∵CF∥DE,
∴∠AFC=∠BEDB,
在△ACF和△BDE中,
|
∴△ACF≌△BDE(AAS),
∴∠A=∠B,
∴AC∥BD.
点评:本题考查了全等三角形的判定和性质,平行线的判定,掌握三角形全等的证明是解题的关键.

练习册系列答案
相关题目
一元二次方程x2-2x-5=0的正整数解的范围是( )
| A、1<x<2 |
| B、2<x<3 |
| C、3<x<4 |
| D、4<x<5 |
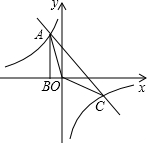 如图,Rt△ABO的顶点A是双曲线y=
如图,Rt△ABO的顶点A是双曲线y= 如图,已知EF∥BC,AE=3,BE=4,FC=6,则AF的值为
如图,已知EF∥BC,AE=3,BE=4,FC=6,则AF的值为