题目内容
 已知:如图,AB是⊙O的直径,AC是⊙O的弦,AB=2,∠BAC=30°.在图中作弦AD,使AD=1,并求∠CAD的度数.
已知:如图,AB是⊙O的直径,AC是⊙O的弦,AB=2,∠BAC=30°.在图中作弦AD,使AD=1,并求∠CAD的度数.考点:圆的认识,等边三角形的判定与性质
专题:分类讨论
分析:利用圆周角定理、圆弧、弧所对的弦的关系,进而得出∠DAB=∠B=60°,进而得出答案.
解答: 解:连接BC,
解:连接BC,
∵AB是⊙O的直径,
∴∠ACB=90°,
∵∠BAC=30°,
∴BC=
AB=1,∠B=60°,
以A圆心BC长为半径画弧可得点D,再连接AD即可;
∵AD=BC,
∴
=
,
∴∠DAB=∠B=60°,
∴∠DAC=60°-30°=30°;
同理可得:∠D′AC=60°+30°=90°;
综上所述:∠CAD的度数为30°或90°.
 解:连接BC,
解:连接BC,∵AB是⊙O的直径,
∴∠ACB=90°,
∵∠BAC=30°,
∴BC=
| 1 |
| 2 |
以A圆心BC长为半径画弧可得点D,再连接AD即可;
∵AD=BC,
∴
 |
| BCD |
 |
| ADC |
∴∠DAB=∠B=60°,
∴∠DAC=60°-30°=30°;
同理可得:∠D′AC=60°+30°=90°;
综上所述:∠CAD的度数为30°或90°.
点评:此题主要考查了圆周角定理以及圆有关的概念,得出∠DAB=∠B=60°是解题关键.

练习册系列答案
相关题目
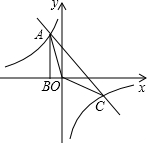 如图,Rt△ABO的顶点A是双曲线y=
如图,Rt△ABO的顶点A是双曲线y=