题目内容
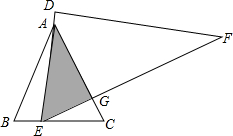 如图,等边△ABC中,AB=6,将一直角三角板DEF的60°角的顶点E置于边BC上移动(不与B、C重合),移动过程中,始终满足直角边DE经过点A,斜边EF交AC于点G.
如图,等边△ABC中,AB=6,将一直角三角板DEF的60°角的顶点E置于边BC上移动(不与B、C重合),移动过程中,始终满足直角边DE经过点A,斜边EF交AC于点G.(1)求证:△ABE∽△ECG;
(2)在移动过程中,线段CG有没有最大值?若有,请求出,若没有,请说明理由.
考点:相似三角形的判定与性质,等边三角形的性质
专题:
分析:(1)根据等边三角形的性质得出∠B=∠C=∠AEG=60°,再求出∠BAE=∠CEG即可;
(2)当AE⊥BC时,CG最大,BE=CE=
BC=3,证明∠AGE=90°,得出CG=
CE=1.5.
(2)当AE⊥BC时,CG最大,BE=CE=
| 1 |
| 2 |
| 1 |
| 2 |
解答:解:(1)证明:∵△ABC是等边三角形,
∴∠B=∠C=∠AEG=60°,
∴∠AEB+∠CEG=180°-∠AEG=120°,∠AEB+∠BAE+=180°-∠B=120°,
∴∠BAE=∠CEG,
∵∠B=∠C,
∴△ABE∽△ECG;
(2)线段CG有最大值;当AE⊥BC时,CG最大;
∵△ABC是等边三角形,AE⊥BC,
∴BE=CE=
BC=3,∠C=60°,
∵∠AEG=60°,
∴∠CEG=90°-60°=30°,
∴∠AGE=90°,
∴CG=
CE=1.5.
∴∠B=∠C=∠AEG=60°,
∴∠AEB+∠CEG=180°-∠AEG=120°,∠AEB+∠BAE+=180°-∠B=120°,
∴∠BAE=∠CEG,
∵∠B=∠C,
∴△ABE∽△ECG;
(2)线段CG有最大值;当AE⊥BC时,CG最大;
∵△ABC是等边三角形,AE⊥BC,
∴BE=CE=
| 1 |
| 2 |
∵∠AEG=60°,
∴∠CEG=90°-60°=30°,
∴∠AGE=90°,
∴CG=
| 1 |
| 2 |
点评:本题考查了三角形相似的判定,解直角三角形,等边三角形的性质以及含30°角的直角三角形的性质等知识点的应用,主要考查学生推理和计算能力,综合性比较强,第二问中得出当AE⊥BC时,CG最大是解题的关键.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
把函数y=x2-4x+6的图象向左平移1个单位,再向上平移1个单位,所得图象对应的函数的解析式是( )
| A、y=(x-3)2+3 |
| B、y=(x-3)2+1 |
| C、y=(x-1)2+3 |
| D、y=(x-1)2+1 |
 如图,在Rt△ABC中,∠C=90°,AC=6,BC=8,D是AB上的动点,E是BC上的动点,则AE+DE的最小值为( )
如图,在Rt△ABC中,∠C=90°,AC=6,BC=8,D是AB上的动点,E是BC上的动点,则AE+DE的最小值为( )A、3+2
| ||
| B、10 | ||
C、
| ||
D、
|
 如图,将矩形纸片ABCD按如图方式折叠,使点D与点B重合,折痕为EF,若S△ABE:S△BFE=4:5,则tan∠BFE=
如图,将矩形纸片ABCD按如图方式折叠,使点D与点B重合,折痕为EF,若S△ABE:S△BFE=4:5,则tan∠BFE= 如图,已知∠AOC=∠DOE=90°,OF平分∠AOD,OB平分∠COE.
如图,已知∠AOC=∠DOE=90°,OF平分∠AOD,OB平分∠COE. 一副三角板按如图所示放置,其中∠F=∠ACB=90°,∠E=30°,∠A=45°,点C在FD的延长线上,点B在DE上.
一副三角板按如图所示放置,其中∠F=∠ACB=90°,∠E=30°,∠A=45°,点C在FD的延长线上,点B在DE上. 先用代数式表示图中阴影部分的面积,再求出当a=15cm,b=10cm时,阴影部分的面积.
先用代数式表示图中阴影部分的面积,再求出当a=15cm,b=10cm时,阴影部分的面积. 如图,正方形A,B,C,D的顶点ABCD都在坐标轴上,已知OA=OB=OC=OD=
如图,正方形A,B,C,D的顶点ABCD都在坐标轴上,已知OA=OB=OC=OD=