题目内容
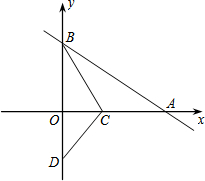 如图:在平面直角坐标系中,直线y=kx+6分别与x轴、y轴交于A、B两点,且OA=8,点C是x轴上一点,如果把△AOB沿着直线BC折叠,那么点A恰好落在y轴负半轴上的点D处.
如图:在平面直角坐标系中,直线y=kx+6分别与x轴、y轴交于A、B两点,且OA=8,点C是x轴上一点,如果把△AOB沿着直线BC折叠,那么点A恰好落在y轴负半轴上的点D处.(1)线段OB的长为
(2)求线段OC的长;
(3)求tan∠ABC的值.
考点:一次函数综合题
专题:
分析:(1)由OA的长得到点A的坐标,代入y=kx+6中求出k的值,从而确定出直线AB的表达式;令直线AB的表达式中的x=0,求出点B的坐标,从而得到OB的长,由OA的长,利用勾股定理求出AB的长,由折叠可知三角形ABC与三角形DBC全等,故AB与BD相等,由BD的长求出OD的长,得到点D的坐标;
(2)由折叠可知三角形ABC与三角形DBC全等,所以∠BAO与∠BDC相等,它们的正切值也相等,根据正切函数定义列出比例式即可求出OC的长;
(4)由折叠可知三角形ABC与三角形DBC全等,所以∠ABC与∠DBC相等,把要求的tan∠ABC转换为tan∠DBC,根据正切函数定义求出值即可.
(2)由折叠可知三角形ABC与三角形DBC全等,所以∠BAO与∠BDC相等,它们的正切值也相等,根据正切函数定义列出比例式即可求出OC的长;
(4)由折叠可知三角形ABC与三角形DBC全等,所以∠ABC与∠DBC相等,把要求的tan∠ABC转换为tan∠DBC,根据正切函数定义求出值即可.
解答:解:(1)由OA=8得到:A(8,0),代入y=kx+6中得:
8k+6=0,解得:k=-
,
∴直线AB的表达式为y=-
x+6;
令x=0得:y=-
×0+6=6,
∴B(0,6),
∴OB=6;
∵OA=8,根据勾股定理得:AB=10,
由折叠可知:△ABC≌△DBC,
∴AB=BD=10,
∴OD=4,
∴点D坐标为(0,-4);
故答案为6,(0,-4).
(2)由折叠可知:△ABC≌△DBC,
∴∠BAO=∠BDC,
则tan∠BAO=tan∠BDC,即
=
,则OC=
=3.
(3)由折叠可知:△ABC≌△DBC,∠ABC=∠DBC,
则tan∠ABC=tan∠DBC=
=
=
.
8k+6=0,解得:k=-
| 3 |
| 4 |
∴直线AB的表达式为y=-
| 3 |
| 4 |
令x=0得:y=-
| 3 |
| 4 |
∴B(0,6),
∴OB=6;
∵OA=8,根据勾股定理得:AB=10,
由折叠可知:△ABC≌△DBC,
∴AB=BD=10,
∴OD=4,
∴点D坐标为(0,-4);
故答案为6,(0,-4).
(2)由折叠可知:△ABC≌△DBC,
∴∠BAO=∠BDC,
则tan∠BAO=tan∠BDC,即
| BO |
| AO |
| OC |
| OD |
| 6×4 |
| 8 |
(3)由折叠可知:△ABC≌△DBC,∠ABC=∠DBC,
则tan∠ABC=tan∠DBC=
| OC |
| OB |
| 3 |
| 6 |
| 1 |
| 2 |
点评:此题考查了全等三角形的性质、三角函数的定义以及一次函数的综合运用.本题的关键是由折叠得三角形全等,利用全等得对应边和对应角相等,借助转化的思想解决数学问题.

练习册系列答案
 新课标阶梯阅读训练系列答案
新课标阶梯阅读训练系列答案 口算心算速算应用题系列答案
口算心算速算应用题系列答案
相关题目
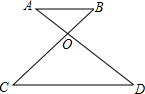 如图,已知AB∥CD,AD与BC相交于点O,AO:DO=1:2,那么下列式子正确的是( )
如图,已知AB∥CD,AD与BC相交于点O,AO:DO=1:2,那么下列式子正确的是( )| A、BO:BC=1:2 |
| B、CD:AB=2:1 |
| C、CO:BC=1:2 |
| D、AD:DO=3:1 |
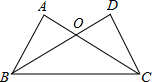 如图,AC与DB相交于点O,已知∠ABC=∠DCB,图中再补充一个条件后可证明△ABC≌△DCB,则这个条件不能是( )
如图,AC与DB相交于点O,已知∠ABC=∠DCB,图中再补充一个条件后可证明△ABC≌△DCB,则这个条件不能是( )| A、AB=DC |
| B、∠A=∠D |
| C、OB=OC |
| D、AC=DB |
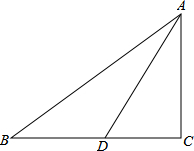 如图,Rt△ABC中,∠C=90°,BD=CD=2,∠ADB=3∠ABD,则AD=
如图,Rt△ABC中,∠C=90°,BD=CD=2,∠ADB=3∠ABD,则AD=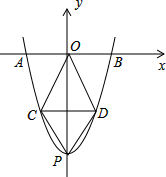 已知抛物线y=x2-8与x轴相交于两点A,B,与y轴相交于点P,
已知抛物线y=x2-8与x轴相交于两点A,B,与y轴相交于点P,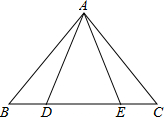 如图D,E是边BC上的两点,AD=AE,∠ADE=∠AED,利用“AAS”方法,请你再添加一个条件:
如图D,E是边BC上的两点,AD=AE,∠ADE=∠AED,利用“AAS”方法,请你再添加一个条件: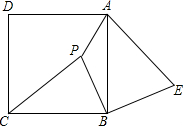 已知:如图,P是正方形ABCD内一点,在正方形ABCD外有一点E,满足∠ABE=∠CBP,BE=BP.
已知:如图,P是正方形ABCD内一点,在正方形ABCD外有一点E,满足∠ABE=∠CBP,BE=BP.