题目内容
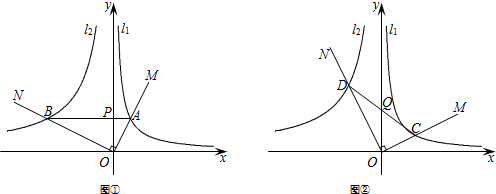
如图①,∠MON=90°,反比例函数y=
(x>0)和y=
(k<0,x<0)的图象分别是l1和l2.射线OM交l1于点A(1,a),射线ON交l2于点B,连接AB交y轴于点P,AB∥x轴.
(1)求k的值;
(2)如图②,将∠MON绕点O旋转,射线OM始终在第一象限,交l1于点C,射线ON交l2于点D,连接CD交y轴于点Q,在旋转的过程中,∠OCD的大小是否发生变化?若不变化,求出tan∠OCD的值;若变化,请说明理由;
(3)在(2)的旋转过程中,当点Q为CD中点时,CD所在的直线与l1的有几个公共点,求出公共点的坐标.
| 2 |
| x |
| k |
| x |
(1)求k的值;
(2)如图②,将∠MON绕点O旋转,射线OM始终在第一象限,交l1于点C,射线ON交l2于点D,连接CD交y轴于点Q,在旋转的过程中,∠OCD的大小是否发生变化?若不变化,求出tan∠OCD的值;若变化,请说明理由;
(3)在(2)的旋转过程中,当点Q为CD中点时,CD所在的直线与l1的有几个公共点,求出公共点的坐标.

考点:反比例函数综合题
专题:
分析:(1)根据自变量的值与函数值的对应关系,可得A点坐标,根据相似三角形的判定与性质,可BP的长,根据待定系数法,可得k值;
(2)根据自变量与函数值的对应关系,可得C点坐标,D点坐标,根据相似三角形的判定与性质,可得
=
,可得m、n的值,根据相似三角形对应变得比相等,可得OD:OC的值,根据正切函数值是定值,可得角是一定的;
(3)根据梯形的中位线,可得m=
,可得C、D的坐标,根据待定系数法,可得CD的解析式,根据两函数解析式,可得方程组,根据解方程组,可得图象的交点坐标.
(2)根据自变量与函数值的对应关系,可得C点坐标,D点坐标,根据相似三角形的判定与性质,可得
| DF |
| OE |
| OF |
| CE |
(3)根据梯形的中位线,可得m=
| 4 |
| m |
解答: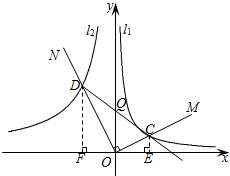 解:(1)将A(1,a)代入y=
解:(1)将A(1,a)代入y=
,得a=2,
∴A(1,2),OP=2,AP=1,
∵AB∥x轴,
∴AB⊥OP,
又∵∠MON=90°,
∴△OPA∽△BPO,
∴
=
,BP=
=4,
∵点B在第二象限,
∴B(-4,2)代入y=
,得k=-8.
(2)∠OCD的大小不变.
过点C作CE⊥x轴于点E,过点D作DF⊥x轴于点F,
设OE=m,OF=n,
∴C(m,
),D(-n,
),
易证△DFO∽△OEC,
∴
=
,
∴
=
,
∴m2n2=16,
∵m>0,n>0,
∴mn=4,n=
,
∵△DFO∽△OEC,
∴
=
,
∴
=
÷
=2,即tan∠OCD=2.
(3)当点Q为CD中点时,OE=OF,
∴m=
,
∵m>0,∴m=2,
∴C(2,1),D(-2,4).
设直线CD的解析式为y=k1x+b,可得
,解得
,
∴直线CD的解析式为y=-
x+
,
联立方程组
,解得
,
.
∴CD所在的直线与l1的有两个公共点,分别是(2,1)和(
,
).
 解:(1)将A(1,a)代入y=
解:(1)将A(1,a)代入y=| 2 |
| x |
∴A(1,2),OP=2,AP=1,
∵AB∥x轴,
∴AB⊥OP,
又∵∠MON=90°,
∴△OPA∽△BPO,
∴
| BP |
| OP |
| PO |
| PA |
| PO2 |
| PA |
∵点B在第二象限,
∴B(-4,2)代入y=
| k |
| x |
(2)∠OCD的大小不变.
过点C作CE⊥x轴于点E,过点D作DF⊥x轴于点F,
设OE=m,OF=n,
∴C(m,
| 2 |
| m |
| 8 |
| n |
易证△DFO∽△OEC,
∴
| DF |
| OE |
| OF |
| CE |
∴
| ||
| m |
| n | ||
|
∴m2n2=16,
∵m>0,n>0,
∴mn=4,n=
| 4 |
| m |
∵△DFO∽△OEC,
∴
| DO |
| OC |
| OF |
| CE |
∴
| DO |
| OC |
| 4 |
| m |
| 2 |
| m |
(3)当点Q为CD中点时,OE=OF,
∴m=
| 4 |
| m |
∵m>0,∴m=2,
∴C(2,1),D(-2,4).
设直线CD的解析式为y=k1x+b,可得
|
|
∴直线CD的解析式为y=-
| 3 |
| 4 |
| 5 |
| 2 |
联立方程组
|
|
|
∴CD所在的直线与l1的有两个公共点,分别是(2,1)和(
| 4 |
| 3 |
| 3 |
| 2 |
点评:本题考查了反比例函数综合题,(1)利用了相似三角形的判定与性质,待定系数法求函数解析式,(2)利用相似三角形的性质得出m、n得出m、n的关系,得出∠OCD的正切值,(3)利用梯形的中位线,得出m的值,再利用自变量与函数值的对定关系,得出点C、D的坐标,利用待定系数法得出直线CD的函数解析式,利用解方程组,得出交点坐标.

练习册系列答案
相关题目
已知a<b,则下列不等式一定成立的是( )
| A、a+3>b+3 |
| B、2a>2b |
| C、-b>-a |
| D、b-a>0 |
△ABC中,AB=AC,AB边的中垂线与直线AC所成的角为50°,则∠B等于( )
| A、70° |
| B、20°或70° |
| C、40°或70° |
| D、40°或20° |
如果方程1=3-2x与关于x的方程2=
的解相同,则a的值为( )
| a-x |
| 3 |
| A、1 | ||
| B、3 | ||
| C、7 | ||
D、
|
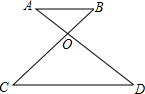 如图,已知AB∥CD,AD与BC相交于点O,AO:DO=1:2,那么下列式子正确的是( )
如图,已知AB∥CD,AD与BC相交于点O,AO:DO=1:2,那么下列式子正确的是( )| A、BO:BC=1:2 |
| B、CD:AB=2:1 |
| C、CO:BC=1:2 |
| D、AD:DO=3:1 |
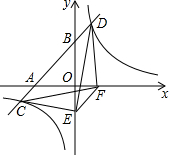 如图,一次函数y=x+3的图象与x轴,y轴交于A、B两点,与反比例函数y=
如图,一次函数y=x+3的图象与x轴,y轴交于A、B两点,与反比例函数y=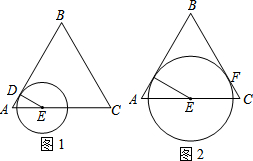 己知等边△ABC,边长为4,点D从点A出发,沿AB运动到点B,到点B停止运动.点E从A出发,沿AC的方向在直线AC上运动.点D的速度为每秒1个单位,点E的速度为每秒2个单位,它们同时出发,同时停止.以点E为圆心,DE长为半径作圆.设E点的运动时间为t秒,
己知等边△ABC,边长为4,点D从点A出发,沿AB运动到点B,到点B停止运动.点E从A出发,沿AC的方向在直线AC上运动.点D的速度为每秒1个单位,点E的速度为每秒2个单位,它们同时出发,同时停止.以点E为圆心,DE长为半径作圆.设E点的运动时间为t秒, 有理数a、b在数轴上的位置如图所示,在下列结论中:
有理数a、b在数轴上的位置如图所示,在下列结论中: