题目内容
1.已知实数x0,y0是方程组$\left\{{\begin{array}{l}{y=\frac{1}{x}}\\{y=|x|+1}\end{array}}\right.$的解,则x0+y0=1或$\sqrt{3}$.分析 当x0<0时,由第二个方程可得到x0+y0的值;当x0>0时,可求得$\frac{1}{{x}_{0}}$-x0,再利用完全平方公式可求得$\frac{1}{{x}_{0}}$+x0,即x0+y0的值.
解答 解:∵x0,y0是方程组$\left\{\begin{array}{l}{y=\frac{1}{x}}\\{y=|x|+1}\end{array}\right.$的解,
∴$\left\{\begin{array}{l}{{y}_{0}=\frac{1}{{x}_{0}}}\\{{y}_{0}={|x}_{0}|+1}\end{array}\right.$,
当x0<0时,则有y0=-x0+1,
∴x0+y0=1;
当x0>0时,则有y0=x0+1,
∴$\frac{1}{{x}_{0}}$-x0=1,
∴($\frac{1}{{x}_{0}}$+x0)2=($\frac{1}{{x}_{0}}$-x0)2+2=3,
∵x0>0,
∴$\frac{1}{{x}_{0}}$+x0>0,
∴$\frac{1}{{x}_{0}}$+x0=$\sqrt{3}$,即x0+y0=$\sqrt{3}$,
综上可知x0+y0的值为1或$\sqrt{3}$.
故答案为:1或$\sqrt{3}$.
点评 本题主要考查解方程组,关键是利用分类思想把方程化为两种情况,再利用整体思想求解即可.注意完全平方公式的灵活运用.

练习册系列答案
 期末集结号系列答案
期末集结号系列答案
相关题目
16.在墙壁上用两个钉子就能固定一根横放的木条,这样做根据的道理是( )
| A. | 两点确定一条直线 | B. | 两点确定一条线段 | ||
| C. | 两点之间,直线最短 | D. | 两点之间,线段最短 |
17.已知x=y,字母m可以取任意有理数,下列等式不一定成立的是( )
| A. | x+m=y+m | B. | x-m=y-m | C. | xm=ym | D. | x+m=x-m |
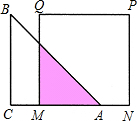 如图,等腰直角△ABC的直角边长与正方形MNPQ的边长均为10cm,AC与MN在同一直线上,开始时A点与M点重合,让向右运动,最后A点与N点重合,则重叠部分面积ycm2与MA长度xcm之间关系式y=$\frac{1}{2}$x2;自变量的取值范围是0<x≤10.
如图,等腰直角△ABC的直角边长与正方形MNPQ的边长均为10cm,AC与MN在同一直线上,开始时A点与M点重合,让向右运动,最后A点与N点重合,则重叠部分面积ycm2与MA长度xcm之间关系式y=$\frac{1}{2}$x2;自变量的取值范围是0<x≤10.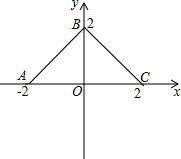 如图,在直角坐标系上有折线段ABC,它们的坐标分别是A(-2,0),B(0,2),C(2,0),若有动直线l:y=t(0<t<2)线段AB交于M,与线段BC交于N,如果记三角形MNO的面积为S.
如图,在直角坐标系上有折线段ABC,它们的坐标分别是A(-2,0),B(0,2),C(2,0),若有动直线l:y=t(0<t<2)线段AB交于M,与线段BC交于N,如果记三角形MNO的面积为S.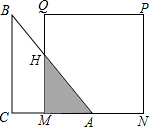 如图,已知等腰直角三角形ABC的直角边长与正方形MNPQ的边长均为20cm,AC与MN在同一条直线上,开始时点A与点N重合,让△ABC以2cm/s的速度向左运动,最终点A与点M重合.求:
如图,已知等腰直角三角形ABC的直角边长与正方形MNPQ的边长均为20cm,AC与MN在同一条直线上,开始时点A与点N重合,让△ABC以2cm/s的速度向左运动,最终点A与点M重合.求: