题目内容
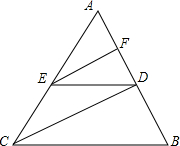 如图,在△ABC中,EF∥CD,DE∥BC,求证:AF•BD=AD•FD.
如图,在△ABC中,EF∥CD,DE∥BC,求证:AF•BD=AD•FD.考点:相似三角形的判定与性质
专题:证明题
分析:如图,由EF∥CD,DE∥BC,得到
=
,
=
,进而得到
=
,即可解决问题.
| AF |
| FD |
| AE |
| ED |
| AD |
| BD |
| AE |
| ED |
| AF |
| FD |
| AD |
| DB |
解答: 证明:∵EF∥CD,DE∥BC,
证明:∵EF∥CD,DE∥BC,
∴
=
,
=
,
∴
=
,
∴AF•BD=AD•FD.
 证明:∵EF∥CD,DE∥BC,
证明:∵EF∥CD,DE∥BC,∴
| AF |
| FD |
| AE |
| ED |
| AD |
| BD |
| AE |
| ED |
∴
| AF |
| FD |
| AD |
| DB |
∴AF•BD=AD•FD.
点评:该题主要考查了平行线分线段成比例定理及其应用问题;解题的关键是深入观察图形,准确找出图形中的对应元素,灵活运用平行线分线段成比例定理来分析、判断、解答.

练习册系列答案
相关题目
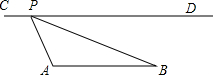 如图,AB∥CD,线段AB与直线CD间的距离为3,AB=8,点P是直线CD上一个动点,则使△ABP为直角三角形的这样的点P的个数为( )
如图,AB∥CD,线段AB与直线CD间的距离为3,AB=8,点P是直线CD上一个动点,则使△ABP为直角三角形的这样的点P的个数为( )| A、1个 | B、2个 | C、4个 | D、5个 |
 如图:在△ABC中,BE、CF分别是AC、AB两边上的高,在BE上截取BD=AC,在CF的延长线上截取CG=AB,连结AD、AG.求证:
如图:在△ABC中,BE、CF分别是AC、AB两边上的高,在BE上截取BD=AC,在CF的延长线上截取CG=AB,连结AD、AG.求证: 如图,它可以看作“
如图,它可以看作“ ”通过连续平移
”通过连续平移 ”绕中心旋转
”绕中心旋转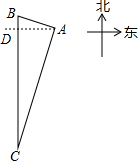 如图,某国3艘炮艇正追袭5条中国渔船,“中国渔政310”船(用“A”表示)接到陆地指挥中心(用“B”表示)命令疾速驰救中国渔船,渔船(用“C”表示)位于陆地指挥中心正南方向.经测定AB=
如图,某国3艘炮艇正追袭5条中国渔船,“中国渔政310”船(用“A”表示)接到陆地指挥中心(用“B”表示)命令疾速驰救中国渔船,渔船(用“C”表示)位于陆地指挥中心正南方向.经测定AB= 如图,在△ABC中,
如图,在△ABC中, 如图,在△ABC中,D、E分别是边AB、AC上的点,DE∥BC,AD:DB=1:2,S△ADE=1,则S四边形BCED的值为
如图,在△ABC中,D、E分别是边AB、AC上的点,DE∥BC,AD:DB=1:2,S△ADE=1,则S四边形BCED的值为