题目内容
进价为每件40元的某商品,售价为每件50元时,每星期可卖出500件,市场调查反映:如果每件的售价每降价1元,每星期可多卖出100件,但售价不能低于每件42元,且每星期至少要销售800件.设每件降价x元 (x为正整数),每星期的利润为y元.
(1)求y与x的函数关系式并写出自变量x的取值范围;
(2)若某星期的利润为5600元,此利润是否是该星期的最大利润?说明理由.
(3)直接写出售价为多少时,每星期的利润不低于5000元?
(1)求y与x的函数关系式并写出自变量x的取值范围;
(2)若某星期的利润为5600元,此利润是否是该星期的最大利润?说明理由.
(3)直接写出售价为多少时,每星期的利润不低于5000元?
考点:二次函数的应用
专题:
分析:(1)根据利润y=每件利润×销售量,每件利润=50-40-x,销售量=500+100x,而售价50-x≥42,销售量=500+100x≥800,列不等式组求x的取值范围;
(2)根据(1)的关系式配方后确定最大利润,与5600比较后即可发现是否为最大利润;
(3)设当y=5000时x有两个解,可推出0≤x≤5时,y≥5000.
(2)根据(1)的关系式配方后确定最大利润,与5600比较后即可发现是否为最大利润;
(3)设当y=5000时x有两个解,可推出0≤x≤5时,y≥5000.
解答:解:(1)依题意,得y=(50-40-x)•(500+100x)=-100x2+500x+5000,
∵
,
∴3≤x≤8;
(2)y=-100x2+500x+5000=-100(x-
)+5625,
∵5600<5625,
∴5600不是最大利润.
(3)当y=5000时,y=-100x2+500x+5000=5000,
解得x1=0,x2=5,
故当0≤x≤5时,y≥5000,
即当售价在不小于45元且不大于50元时,月利润不低于5000元.
∵
|
∴3≤x≤8;
(2)y=-100x2+500x+5000=-100(x-
| 5 |
| 2 |
∵5600<5625,
∴5600不是最大利润.
(3)当y=5000时,y=-100x2+500x+5000=5000,
解得x1=0,x2=5,
故当0≤x≤5时,y≥5000,
即当售价在不小于45元且不大于50元时,月利润不低于5000元.
点评:本题考查点的坐标的求法及二次函数的实际应用.此题为数学建模题,借助二次函数解决实际问题.

练习册系列答案
相关题目
小明由等积式5x=6y写了以下比例式:①
=
;②
=
;③
=
;④
=
,则小明写出的比例式中正确的是( )
| y |
| x |
| 5 |
| 6 |
| x |
| y |
| 5 |
| 6 |
| x |
| 6 |
| y |
| 5 |
| 5 |
| x |
| y |
| 6 |
| A、①③ | B、②③ | C、②④ | D、③④ |
已知k1<0<k2,则函数y=k1x和y=
的图象大致是( )
| k2 |
| x |
A、 |
B、 |
C、 |
D、 |
 如图,画AE⊥DC,DF⊥BC,垂足分别为点E,F.
如图,画AE⊥DC,DF⊥BC,垂足分别为点E,F.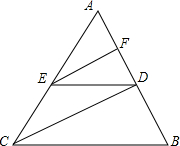 如图,在△ABC中,EF∥CD,DE∥BC,求证:AF•BD=AD•FD.
如图,在△ABC中,EF∥CD,DE∥BC,求证:AF•BD=AD•FD.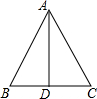 若正三角形的边长为2
若正三角形的边长为2 如图,OX和OY分别为点O向外延伸的射线,在OX,OY上分别取点A、B,将A、B相连,∠XOA=60°,BC为∠XBA的角平分线,BC的反向延长线与∠BAO的角平分线相交于点D.如果A、B分别可以在OY与OX上随意移动,求∠CDA的度数,如果没有固定值,请写出取值范围.
如图,OX和OY分别为点O向外延伸的射线,在OX,OY上分别取点A、B,将A、B相连,∠XOA=60°,BC为∠XBA的角平分线,BC的反向延长线与∠BAO的角平分线相交于点D.如果A、B分别可以在OY与OX上随意移动,求∠CDA的度数,如果没有固定值,请写出取值范围.