题目内容
 如图,在△ABC中,
如图,在△ABC中,| AG |
| DE |
| AH |
| BC |
考点:相似三角形的判定与性质
专题:
分析:由
=
,得出
=
,求出
=
,即可求出AH的长.
| AG |
| DE |
| AH |
| BC |
| AG |
| AH |
| DE |
| BC |
| GH |
| AH |
| 1 |
| 5 |
解答:解:∵
=
,
∴
=
,
即
=
=
,
∴
=
,
∴
=
,
∴AH=40.
| AG |
| DE |
| AH |
| BC |
∴
| AG |
| AH |
| DE |
| BC |
即
| AG |
| AH |
| 24 |
| 30 |
| 4 |
| 5 |
∴
| GH |
| AH |
| 1 |
| 5 |
∴
| 8 |
| AH |
| 1 |
| 5 |
∴AH=40.
点评:本题考查了比例的性质;根据比例的性质进行变式计算是解题的关键.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
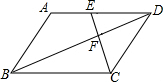 如图,在平行四边形ABCD中,点E是边AD上的一点,且AE:ED=2:3,EC交对角线BD于点F,则EF:FC等于( )
如图,在平行四边形ABCD中,点E是边AD上的一点,且AE:ED=2:3,EC交对角线BD于点F,则EF:FC等于( )| A、3:2 | B、2:5 |
| C、2:3 | D、3:5 |
要由抛物线y=5x2得到抛物线y=5(x-1)2+3,则抛物线y=5x2必须( )
| A、向左平移1个单位,再向下平移3个单位 |
| B、向右平移1个单位,再向上平移3个单位 |
| C、向右平移1个单位,再向下平移3个单位 |
| D、向左平移1个单位,再向上平移3个单位 |
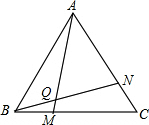 △ABC为等边三角形,点M是射线BC上一点,点N是CA上一点,且BM=CN,BN与AM相交于Q点.
△ABC为等边三角形,点M是射线BC上一点,点N是CA上一点,且BM=CN,BN与AM相交于Q点. 如图,如果∠AOB=155°,∠AOC=∠BOD=90°,则∠COD=
如图,如果∠AOB=155°,∠AOC=∠BOD=90°,则∠COD=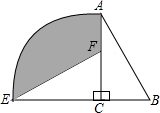 如图,在平面内将Rt△ABC绕着直角顶点C逆时针旋转90°,得到Rt△EFC,若AB=
如图,在平面内将Rt△ABC绕着直角顶点C逆时针旋转90°,得到Rt△EFC,若AB=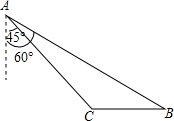 如图,到海岛景区C有两条旅游线路可供选择,游人可从码头A乘游艇或从码头B乘游船前往,已知B在A南偏东60°方向,C位于A南偏东45°方向10海里处,且C在B正西方向,游艇的速度为每小时30海里,游船的速度为每小时13海里,问游客选择哪条线路用时较少?并说明理由.(参考数据:
如图,到海岛景区C有两条旅游线路可供选择,游人可从码头A乘游艇或从码头B乘游船前往,已知B在A南偏东60°方向,C位于A南偏东45°方向10海里处,且C在B正西方向,游艇的速度为每小时30海里,游船的速度为每小时13海里,问游客选择哪条线路用时较少?并说明理由.(参考数据: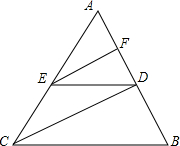 如图,在△ABC中,EF∥CD,DE∥BC,求证:AF•BD=AD•FD.
如图,在△ABC中,EF∥CD,DE∥BC,求证:AF•BD=AD•FD. 如图,OX和OY分别为点O向外延伸的射线,在OX,OY上分别取点A、B,将A、B相连,∠XOA=60°,BC为∠XBA的角平分线,BC的反向延长线与∠BAO的角平分线相交于点D.如果A、B分别可以在OY与OX上随意移动,求∠CDA的度数,如果没有固定值,请写出取值范围.
如图,OX和OY分别为点O向外延伸的射线,在OX,OY上分别取点A、B,将A、B相连,∠XOA=60°,BC为∠XBA的角平分线,BC的反向延长线与∠BAO的角平分线相交于点D.如果A、B分别可以在OY与OX上随意移动,求∠CDA的度数,如果没有固定值,请写出取值范围.