题目内容
13.先化简再求值:$\frac{3x-3}{x^2-1}$÷$\frac{3x}{x+1}$-$\frac{1}{x-1}$,已知x满足x2-x-1=0.分析 首先把已知的分式分子分母分解因式,把除法转化为乘法,计算乘法,然后计算分式的减法即可化简,然后代入求解即可.
解答 解:原式=$\frac{3(x-1)}{(x+1)(x-1)}$•$\frac{x+1}{3x}$-$\frac{1}{x-1}$
=$\frac{1}{x}$-$\frac{1}{x-1}$
=$\frac{x-1-x}{x(x-1)}$
=-$\frac{1}{{x}^{2}-x}$,
∵x2-x-1=0,
∴x2-x=1,
∴原式=-1.
点评 此题主要考查了方程解的定义和分式的运算,此类题型的特点是:利用方程解的定义找到相等关系,再把所求的代数式化简后整理出所找到的相等关系的形式,再把此相等关系整体代入所求代数式,即可求出代数式的值.

练习册系列答案
 英语小英雄天天默写系列答案
英语小英雄天天默写系列答案 暑假作业安徽少年儿童出版社系列答案
暑假作业安徽少年儿童出版社系列答案
相关题目
4.在分式$\frac{a}{b+c}$中,a,b,c都缩小到原来的一半,则分式的值是原来的( )
| A. | 1倍 | B. | 一半 | C. | 2倍 | D. | 4倍 |
2.当|k-2b|+$\sqrt{k+b-3}$=0时,直线y=kx+b经过点( )
| A. | (-1,-1) | B. | (-1,1) | C. | (-1,-3) | D. | (-1,3) |
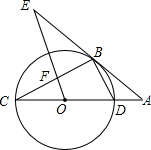 如图所示,CD为⊙O的直径,点B在⊙O上,连接BC、BD,过点B的切线AE与CD的延长线交于点A,OE∥BD,交BC于点F,交AB于点E.
如图所示,CD为⊙O的直径,点B在⊙O上,连接BC、BD,过点B的切线AE与CD的延长线交于点A,OE∥BD,交BC于点F,交AB于点E.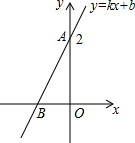 如图所示,直线AB是一次函数y=kx+b的图象.若AB=$\sqrt{5}$,则函数解析式为y=2x+2.
如图所示,直线AB是一次函数y=kx+b的图象.若AB=$\sqrt{5}$,则函数解析式为y=2x+2.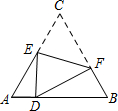 如图,D是等边△ABC边AB上的一点,且AD:DB=1:3,现将△ABC折叠,使点C与D重合,折痕为EF,点E,F分别在AC和BC上,则CE:CF=5:7.
如图,D是等边△ABC边AB上的一点,且AD:DB=1:3,现将△ABC折叠,使点C与D重合,折痕为EF,点E,F分别在AC和BC上,则CE:CF=5:7.