题目内容
19.甲、乙两辆卡车匀速行驶在某公路上.(1)如果甲车以60km/h的速度从某地出发,写出它行驶的路程s1(km)和它的行驶时间t(h)之间的函数表达式,并画出它的图象;
(2)如果乙车在甲车出发2h后从同一地点出发,沿同一方向以80km/h的速度行驶,它行驶的路程s2(km)也是甲车出发后的行驶时间t(h)的函数,写出它的表达式,并在前一个坐标系中画出它的图象;
(3)求出两图象交点的坐标,并说明交点坐标的实际意义.
分析 (1)根据题意列出函数解析式,画出图象即可;
(2)根据题意列出函数解析式,画出图象即可;
(3)联立方程组解答即可.
解答 解:(1)它行驶的路程s1(km)和它的行驶时间t(h)之间的函数表达式为s1=60t,图象如图1:
(2)它行驶的路程s2(km)也是甲车出发后的行驶时间t(h)的函数表达式为s2=80t-160,图象如图1:
(3)联立方程可得:60t=80t-160,
解得:t=8,
交点坐标为(8,480),实际意义为:当t=8时,甲乙两车相遇.
点评 本题考查了一次函数的应用,主要利用了待定系数法求函数解析式,路程、时间、速度三者之间的关系,从图中准确获取信息是解题的关键.

练习册系列答案
相关题目
11.下列运算正确的是( )
| A. | (3x2)3=9x6 | B. | a6÷a2=a3 | C. | (a+b)2=a2+b2 | D. | (a-b)(a+b)=a2-b2 |
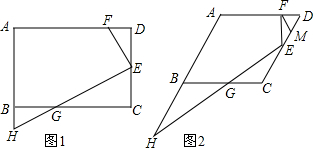
8. 如图,点C在以AB为直径的半圆上,AB=2,∠CBA=30°,点D到线段AB上运动,点E与点D关于AC对称,DF⊥DE,DF交EC的延长线于点F,当点D从点A运动到点B时,线段EF扫过的面积是( )
如图,点C在以AB为直径的半圆上,AB=2,∠CBA=30°,点D到线段AB上运动,点E与点D关于AC对称,DF⊥DE,DF交EC的延长线于点F,当点D从点A运动到点B时,线段EF扫过的面积是( )
 如图,点C在以AB为直径的半圆上,AB=2,∠CBA=30°,点D到线段AB上运动,点E与点D关于AC对称,DF⊥DE,DF交EC的延长线于点F,当点D从点A运动到点B时,线段EF扫过的面积是( )
如图,点C在以AB为直径的半圆上,AB=2,∠CBA=30°,点D到线段AB上运动,点E与点D关于AC对称,DF⊥DE,DF交EC的延长线于点F,当点D从点A运动到点B时,线段EF扫过的面积是( )| A. | $\frac{\sqrt{3}}{3}$ | B. | $\frac{\sqrt{3}}{2}$ | C. | $\sqrt{3}$ | D. | 2$\sqrt{3}$ |

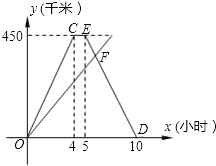 A、B两地间的公路长为450千米,甲、乙两车同时从A地出发沿这一公路驶向B地,甲车到达1小时后沿原路返回,如图是它们离A地的距离y(千米)与行驶时间x(小时)之间的函数图象.
A、B两地间的公路长为450千米,甲、乙两车同时从A地出发沿这一公路驶向B地,甲车到达1小时后沿原路返回,如图是它们离A地的距离y(千米)与行驶时间x(小时)之间的函数图象. 一列快车从甲地驶往乙地,一列慢车从乙地驶往甲地,两车同时出发,设慢车行驶的时间为x(h),两车之间的距离为y(km),图中的折线表示y与x之间的函数关系.根据图象进行以下探究:
一列快车从甲地驶往乙地,一列慢车从乙地驶往甲地,两车同时出发,设慢车行驶的时间为x(h),两车之间的距离为y(km),图中的折线表示y与x之间的函数关系.根据图象进行以下探究: 在正方形ABCD处,以BC为边作一个等边三角形△BCE,则∠DCE=150°.
在正方形ABCD处,以BC为边作一个等边三角形△BCE,则∠DCE=150°.