题目内容
18.已知正方形ABCD,E为平面内任意一点,连结DE,将线段DE绕点D顺时针旋转90°得到DG,连结EC,AG.(1)当点E在正方形ABCD内部时,
①依题意补全图形;
②判断AG与CE的数量关系与位置关系并写出证明思路.
(2)当点B,D,G在一条直线时,若AD=4,DG=$\sqrt{2}$,求CE的长.

分析 (1)依题意补全图形,如图1所示,
(2)由旋转得到∠GDA=∠EDC,判断出△AGD≌△CED,得出∠AFH=∠HDC=90°即可;
(3)由正方形的线段得到MD=MG=1,再根据勾股定理计算即可.
解答 证明:(1)
①依题意补全图形,如图1所示,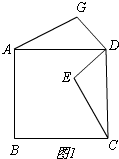
②AG=CE,AG⊥CE.
证明思路如下: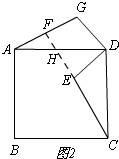
由正方形ABCD,可得AD=CD,∠ADC=90°,
由DE绕着点D顺时针旋转90°得DG,
∴∠GDE=∠ADC=90°,GD=DE
∴∠GDA=∠EDC.
∵DG=DE,AD=CD,
∴△AGD≌△CED,
∴AG=CE.
延长CE分别交AG、AD于点F、H,
∵△AGD≌△CED,
∴∠GAD=∠ECD,
∵∠AHF=∠CHD,
∴∠AFH=∠HDC=90°
∴AG⊥CH.
(2)当点G在线段BD的延长线上时,如图3所示.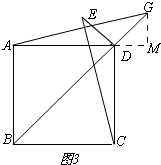
过G作GM⊥AD于M.
∵BD是正方形ABCD的对角线,
∴∠ADB=∠GDM=45°.
∵GM⊥AD,DG=$\sqrt{2}$,
∴MD=MG=1
在Rt△AMG中,由勾股定理,得AG=$\sqrt{A{M}^{2}+M{G}^{2}}$=$\sqrt{26}$
∴CE=AG=$\sqrt{26}$
当点G在线段BD上时,如图4所示.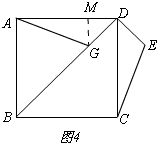
过G作GM⊥AD于M.
∵BD是正方形ABCD的对角线,
∴∠ADG=45°
∵GM⊥AD,DG=$\sqrt{2}$,
∴MD=MG=1
在Rt△AMG中,由勾股定理,得AG=$\sqrt{A{M}^{2}+M{G}^{2}}$=$\sqrt{10}$,
∴CE=AG=$\sqrt{10}$
故CE的长为$\sqrt{26}$或$\sqrt{10}$.
点评 此题是几何变换综合题,主要考查了旋转的性质,全等三角形的性质和判定,勾股定理,判定三角形全等是解本题的关键.

 名校课堂系列答案
名校课堂系列答案 如图,在△ABC中,D,E两点分别在边AB,AC上,AB=8cm,AC=6cm,AD=3cm,要使△ADE与△ABC相似,则线段AE的长为4或$\frac{9}{4}$cm.
如图,在△ABC中,D,E两点分别在边AB,AC上,AB=8cm,AC=6cm,AD=3cm,要使△ADE与△ABC相似,则线段AE的长为4或$\frac{9}{4}$cm.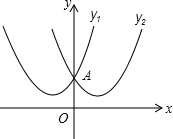 定义感知:我们把顶点关于y轴对称,且交于y轴上同一点的两条抛物线叫做“孪生抛物线”,该点叫“孪生抛物线”的“共点”.如图所示的抛物线y1=x2+2x+2与y2=x2-2x+2是一对“孪生抛物线”,其“共点”为点A.
定义感知:我们把顶点关于y轴对称,且交于y轴上同一点的两条抛物线叫做“孪生抛物线”,该点叫“孪生抛物线”的“共点”.如图所示的抛物线y1=x2+2x+2与y2=x2-2x+2是一对“孪生抛物线”,其“共点”为点A.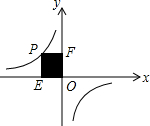 如图,点P是反比例函数在第二象限上的一点,且矩形PEOF的面积为5,则反比例函数的表达式为y=-$\frac{5}{x}$.
如图,点P是反比例函数在第二象限上的一点,且矩形PEOF的面积为5,则反比例函数的表达式为y=-$\frac{5}{x}$.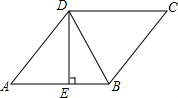 如图,在菱形ABCD中,DE⊥AB,cosA=$\frac{4}{5}$,BE=2,则tan∠DBE=3.
如图,在菱形ABCD中,DE⊥AB,cosA=$\frac{4}{5}$,BE=2,则tan∠DBE=3.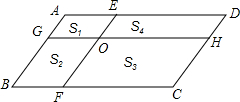 如图,在平行四边形ABCD中,AB∥EF,AD∥GH,EF与GH交于点O,分别的4个小平行四边形的面积分别为S1,S2,S3,S4,若S1=8,S2=10,S3=30,则S4=24.
如图,在平行四边形ABCD中,AB∥EF,AD∥GH,EF与GH交于点O,分别的4个小平行四边形的面积分别为S1,S2,S3,S4,若S1=8,S2=10,S3=30,则S4=24.