题目内容
9. 在正方形ABCD处,以BC为边作一个等边三角形△BCE,则∠DCE=150°.
在正方形ABCD处,以BC为边作一个等边三角形△BCE,则∠DCE=150°.
分析 由正方形的性质和等边三角形的性质得出∠BCD及∠BCE的度数,即可得出∠DCE的度数.
解答 解:∵四边形ABCD是正方形,
∴∠BCD=90°,
∵△BCE是等边三角形,
∴∠BCE=60°,
∴∠DCE=∠BCD+∠BCE=90°+60°=150°,
故答案为:150°.
点评 本题考查了正方形的性质及等边三角形的性质;熟记正方形和等边三角形的性质是解答本题的关键.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
20.下列运算正确的是( )
| A. | 3a2-a2=2 | B. | a2•a3=a6 | C. | (-a2)2=a4 | D. | (a+1)2=a2+1 |
4.下列运算正确的是( )
| A. | -$\frac{5}{7}$+$\frac{2}{7}$=1 | B. | 3÷$\frac{5}{4}$×$\frac{4}{5}$=3÷1=3 | C. | -7-2×5=-9×5=-45 | D. | 0-(-22)=22 |
14.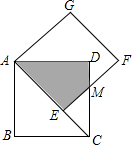 如图,正方形AEFG的边AE放置在正方形ABCD的对角线AC上,EF与CD交于点M,得四边形AEMD,且两正方形的边长均为2,则两正方形重合部分(阴影部分)的面积为( )
如图,正方形AEFG的边AE放置在正方形ABCD的对角线AC上,EF与CD交于点M,得四边形AEMD,且两正方形的边长均为2,则两正方形重合部分(阴影部分)的面积为( )
 如图,正方形AEFG的边AE放置在正方形ABCD的对角线AC上,EF与CD交于点M,得四边形AEMD,且两正方形的边长均为2,则两正方形重合部分(阴影部分)的面积为( )
如图,正方形AEFG的边AE放置在正方形ABCD的对角线AC上,EF与CD交于点M,得四边形AEMD,且两正方形的边长均为2,则两正方形重合部分(阴影部分)的面积为( )| A. | -4+4$\sqrt{2}$ | B. | 4$\sqrt{2}$+4 | C. | 8-4$\sqrt{2}$ | D. | $\sqrt{2}$+1 |
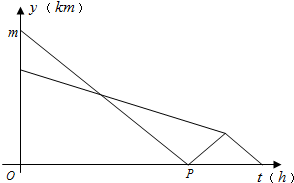 某部队凌晨5:00乘车从住宿地匀速赶往离住宿地90千米的B处执行任务,出发20分钟后在途中遇到提前出发的先遣分队.部队6:00到达B处后,空车原速返回接应先遣分队于6:40准时到达B处.已知汽车和先遣分队距离B处的距离y(km)与汽车行驶时间t(h)的函数关系图象如图所示.
某部队凌晨5:00乘车从住宿地匀速赶往离住宿地90千米的B处执行任务,出发20分钟后在途中遇到提前出发的先遣分队.部队6:00到达B处后,空车原速返回接应先遣分队于6:40准时到达B处.已知汽车和先遣分队距离B处的距离y(km)与汽车行驶时间t(h)的函数关系图象如图所示.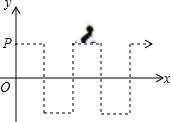 如图,在直角坐标系中,一只蚂蚁从点P(0,1)出发,沿着图示折线方向移动,第一次到达点(1,1),第二次达到点(1,0),第三次达到点(1,-1),第四次达到点(2,-1),…,按照这样的规律,第2016次到达点的坐标应为(672,1).
如图,在直角坐标系中,一只蚂蚁从点P(0,1)出发,沿着图示折线方向移动,第一次到达点(1,1),第二次达到点(1,0),第三次达到点(1,-1),第四次达到点(2,-1),…,按照这样的规律,第2016次到达点的坐标应为(672,1).