题目内容
7.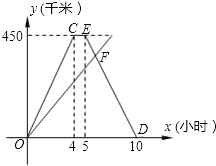 A、B两地间的公路长为450千米,甲、乙两车同时从A地出发沿这一公路驶向B地,甲车到达1小时后沿原路返回,如图是它们离A地的距离y(千米)与行驶时间x(小时)之间的函数图象.
A、B两地间的公路长为450千米,甲、乙两车同时从A地出发沿这一公路驶向B地,甲车到达1小时后沿原路返回,如图是它们离A地的距离y(千米)与行驶时间x(小时)之间的函数图象.(1)甲车返回过程中y与x之间的函数关系式,写出自变量x的取值范围;
(2)乙车行驶6小时与返回的甲车相遇,求乙车的行驶速度;
(3)请你直接写出经过几小时两车之间的距离是150千米?
分析 (1)设出一次函数解析式,代入图象上的两个点的坐标,即可解答;
(2)把x=6代入(1)中的函数解析式,求得路程(甲、乙距A城的距离),进一步求得速度即可解答;
(3)根据两车之间的距离是150千米分几种情况解答.
解答 解:(1)设甲车返回过程中y与x之间的函数解析式y=kx+b,
∵图象过(5,450),(10,0)两点,
∴$\left\{\begin{array}{l}{5k+b=450}\\{10k+b=0}\end{array}\right.$,
解得$\left\{\begin{array}{l}{k=-90}\\{b=900}\end{array}\right.$,
∴y=-90x+900,函数的定义域为5≤x≤10;
(2)当x=6时,y=-90×6+900=360,
${v}_{乙}=\frac{360}{6}=60$(千米/小时).
(3)设OC直线解析式为:y=kx,
把(4,450)代入y=kx中,解得:k=112.5,
所以解析式为:y=112.5x,
当两车之间的距离是150千米,可得:112.5x-60x=150,
解得:x=$\frac{20}{7}$,
当两车之间的距离是150千米,可得:60x-(-90x+900)=150,
解得:x=7,
经过$\frac{20}{7}$、7小时两车之间的距离是150千米
点评 此题主要考查利用待定系数法求函数解析式,以及基本数量关系:路程÷时间=速度,解答时注意数形结合.

练习册系列答案
相关题目
2.若a为有理数,则(a3)2的值为( )
| A. | 有理数 | B. | 正数 | C. | 零或负数 | D. | 正数或零 |
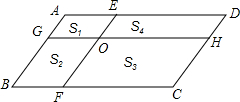 如图,在平行四边形ABCD中,AB∥EF,AD∥GH,EF与GH交于点O,分别的4个小平行四边形的面积分别为S1,S2,S3,S4,若S1=8,S2=10,S3=30,则S4=24.
如图,在平行四边形ABCD中,AB∥EF,AD∥GH,EF与GH交于点O,分别的4个小平行四边形的面积分别为S1,S2,S3,S4,若S1=8,S2=10,S3=30,则S4=24.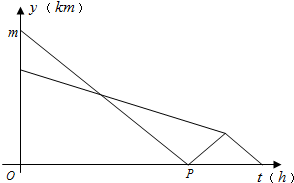 某部队凌晨5:00乘车从住宿地匀速赶往离住宿地90千米的B处执行任务,出发20分钟后在途中遇到提前出发的先遣分队.部队6:00到达B处后,空车原速返回接应先遣分队于6:40准时到达B处.已知汽车和先遣分队距离B处的距离y(km)与汽车行驶时间t(h)的函数关系图象如图所示.
某部队凌晨5:00乘车从住宿地匀速赶往离住宿地90千米的B处执行任务,出发20分钟后在途中遇到提前出发的先遣分队.部队6:00到达B处后,空车原速返回接应先遣分队于6:40准时到达B处.已知汽车和先遣分队距离B处的距离y(km)与汽车行驶时间t(h)的函数关系图象如图所示.