题目内容
4. 一列快车从甲地驶往乙地,一列慢车从乙地驶往甲地,两车同时出发,设慢车行驶的时间为x(h),两车之间的距离为y(km),图中的折线表示y与x之间的函数关系.根据图象进行以下探究:
一列快车从甲地驶往乙地,一列慢车从乙地驶往甲地,两车同时出发,设慢车行驶的时间为x(h),两车之间的距离为y(km),图中的折线表示y与x之间的函数关系.根据图象进行以下探究:(1)甲、乙两地之间的距离为900km;
(2)请解释图中点B和点C的实际意义:答:当慢车行驶4h时,慢车和快车相遇;
(3)慢车的速度是75km/h,快车的速度是150km/h;
(4)求线段BC所表示的y玉x之间的函数关系式,并写出自变量x的取值范围.
分析 (1)由函数图象可以直接求出甲乙两地之间的距离;
(2)由函数图象的数据就可以得出点B的实际意义;
(3)由函数图象的数据,根据速度=路程÷时间就可以得出慢车的速度,由相遇问题求出速度和就可以求出快车的速度进而得出结论;
(4)由快车的速度求出快车走完全程的时间就可以求出点C的横坐标,由两车的距离=速度和×时间就可以求出C点的纵坐标,由待定系数法就可以求出结论
解答 解:(1)由题意,得
甲、乙两地之间的距为900km.
故答案为:900;
(2)由函数图象,得图中点B的实际意义是:当慢车行驶4 h时,慢车和快车相遇.
故答案为:当慢车行驶4 h时,慢车和快车相遇;
(3)由题意,得
快车与慢车的速度和为:900÷4=225km/h,
慢车的速度为:900÷12=75km/h,
快车的速度为:225-75=150 km/h.
答:快车的速度为150km/h,慢车的速度为75km/h,
故答案为:75;150;
(4)由题意,得快车走完全程的时间按为:900÷150=6h,
6时时两车之间的距离为:225×(6-4)=450km.
则C(6,450).
设线段BC的解析式为y=kx+b,由题意,得
$\left\{\begin{array}{l}{0=4k+b}\\{450=6k+b}\end{array}\right.$,
解得:$\left\{\begin{array}{l}{k=225}\\{b=900}\end{array}\right.$,
则y=225x-900,自变量x的取值范围是4≤x≤6
点评 本题考查了行程问题的数量关系路程÷时间=速度的运用,待定系数法求一次函数的解析式的运用,相遇问题的数量关系的运用,解答时求出一次函数的解析式是关键.

练习册系列答案
 期末宝典单元检测分类复习卷系列答案
期末宝典单元检测分类复习卷系列答案
相关题目
13.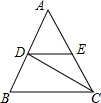 如图,在△ABC中,∠ACB的平分线交AB于点D,点E在AC上,DE∥BC,若∠CDE=30°,则∠AED=( )
如图,在△ABC中,∠ACB的平分线交AB于点D,点E在AC上,DE∥BC,若∠CDE=30°,则∠AED=( )
 如图,在△ABC中,∠ACB的平分线交AB于点D,点E在AC上,DE∥BC,若∠CDE=30°,则∠AED=( )
如图,在△ABC中,∠ACB的平分线交AB于点D,点E在AC上,DE∥BC,若∠CDE=30°,则∠AED=( )| A. | 50° | B. | 60° | C. | 70° | D. | 80° |
14.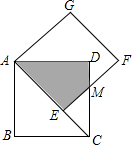 如图,正方形AEFG的边AE放置在正方形ABCD的对角线AC上,EF与CD交于点M,得四边形AEMD,且两正方形的边长均为2,则两正方形重合部分(阴影部分)的面积为( )
如图,正方形AEFG的边AE放置在正方形ABCD的对角线AC上,EF与CD交于点M,得四边形AEMD,且两正方形的边长均为2,则两正方形重合部分(阴影部分)的面积为( )
 如图,正方形AEFG的边AE放置在正方形ABCD的对角线AC上,EF与CD交于点M,得四边形AEMD,且两正方形的边长均为2,则两正方形重合部分(阴影部分)的面积为( )
如图,正方形AEFG的边AE放置在正方形ABCD的对角线AC上,EF与CD交于点M,得四边形AEMD,且两正方形的边长均为2,则两正方形重合部分(阴影部分)的面积为( )| A. | -4+4$\sqrt{2}$ | B. | 4$\sqrt{2}$+4 | C. | 8-4$\sqrt{2}$ | D. | $\sqrt{2}$+1 |
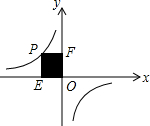 如图,点P是反比例函数在第二象限上的一点,且矩形PEOF的面积为5,则反比例函数的表达式为y=-$\frac{5}{x}$.
如图,点P是反比例函数在第二象限上的一点,且矩形PEOF的面积为5,则反比例函数的表达式为y=-$\frac{5}{x}$.